Kezdőlap


Feladat:	117. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bollobás Béla , Fritz József , Góth László , Nagy Dezső , Sonnevend György , Zakariás L.
Füzet:	1961/május, 236 - 237. oldal		PDF \| MathML
Témakör(ök):	Bernoulli-törvény, Hajítások, Feladat
Hivatkozás(ok):	Feladatok: 1961/január: 117. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Helyezzük el a koordináta-rendszert az ábrán látható módon.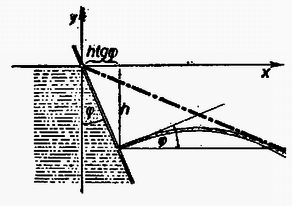

A vízfelszín alatt

h

mélységben a vízsugár a falra merőlegesen

\sqrt[]{2 g h}

sebességgel lép ki. A fal

h

mélységű pontjához

h tg φ

abszcissza tartozik, így

t

idő múlva a vízrészecske koordinátái, a merőleges szárú szögeket figyelembevéve:

\begin{matrix} x = h tg φ + t \sqrt[]{2 g h} cos φ, \\ y = - h + t \sqrt[]{2 g h} sin φ - \frac{g}{2} t^{2} . \end{matrix}

Az első egyenletből

t

-t kifejezve az egyenletrendszerből

t

-t kiküszöböljük, majd a kapott egyenletet

h

szerint rendezzük:

\begin{matrix} h^{2} (4 + {tg}^{2} φ) - h [2 x (sin 2 φ + tg φ) - 4 y cos^{2} φ] + x^{2} = 0. \end{matrix}

A burkológörbét azon

(x, y)

pontok alkotják, amelyekhez csak egy lyukból (vagyis egy

h

mellett) juthat el a vízsugár. Tehát a burkológörbe egyenletét megkapjuk, ha ezen

h

-ban másodfokú egyenlet diszkriminánsát

0

-val tesszük egyenlővé:

\begin{matrix} ^{2} = 4 x^{2} (4 + {tg}^{2} φ), \\ 2 x (sin 2 φ + tg φ) - 4 y cos^{2} φ = \pm 2 x \sqrt[]{4 + {tg}^{2} φ}, ebből \\ y = \frac{tg φ + sin 2 φ \mp \sqrt[]{4 + {tg}^{2} φ}}{2 cos^{2} φ} x . \end{matrix}

Ha a feladatot úgy értelmezzük, hogy az edény oldalfala a vízfelszínnel tompaszöget zár be, akkor az ábra alapján könnyen megállapíthatjuk, hogy a kapott egyenes iránytangensének negatívnak kell lennie, így szükségképpen a burkológörbe az origón átmenő olyan egyenes, amelynek egyenlete:

\begin{matrix} y = \frac{tg φ + sin 2 φ - \sqrt[]{4 + {tg}^{2} φ}}{2 cos^{2} φ} x . \end{matrix}

Nagy Dezső (Bp., Piarista g. IV. o. t.)

II. megoldás: Tekintve, hogy

t

időpillanatban a vízrészecske sebességének vízszintes komponense

\sqrt[]{2 g h} cos φ

, függőleges komponense

\sqrt[]{2 g h} sin φ - g t

, a parabolák érintőjének iránytangense

t

függvényeként

\begin{matrix} m = \frac{\sqrt[]{2 g h} sin φ - g t}{\sqrt[]{2 g h} cos φ} = tg φ - \frac{g}{\sqrt[]{2 g h} cos φ} t, innen \\ t = - \frac{\sqrt[]{2 g h}}{g} cos φ (m - tg φ) . \end{matrix}

Ezzel a

t

paramétert kiküszöböljük:

\begin{matrix} x = h tg φ - \frac{2 g h}{g} cos^{2} φ (m - tg φ) = h (tg φ - 2 m cos^{2} φ + sin 2 φ), \\ y = - h - \frac{2 g h}{g} sin φ cos φ (m - tg φ) - \frac{g}{2} \cdot \frac{2 g h}{g^{2}} cos^{2} φ {(m - tg φ)}^{2} = \\ = h (- 1 - m sin 2 φ + 2 sin^{2} φ - m^{2} cos^{2} φ + m sin 2 φ - 2 sin^{2} φ) = \\ = - h cos^{2} φ (1 + m^{2}) . \end{matrix}

Így

y / x = f (m)

h

-tól független (a

φ

-t rögzítettnek képzeljük); ez azt jelenti, hogy valamennyi parabolának

m

iránytangensű érintőjén levő pontja az

y = f (m) \cdot x

egyenesen van. Tehát, ha

f (m) = m

, akkor a parabolasereg minden egyes tagja érinti az

y = m x

egyenest, azaz ez a burkológörbe.
Határozzuk meg

m

-et az

f (m) = m

egyenletből !

\begin{matrix} - cos^{2} φ - m^{2} cos^{2} φ = m tg φ - 2 m^{2} cos^{2} φ + m sin 2 φ, \\ m^{2} cos^{2} φ - m (tg φ + sin 2 φ) - cos^{2} φ = 0, innen \end{matrix}

trigonometriai átalakításokkal:

\begin{matrix} m = \frac{tg φ + sin 2 φ - \sqrt[]{{(tg φ + sin 2 φ)}^{2} + 4 cos^{4} φ}}{2 cos^{2} φ} = \frac{tg φ + sin 2 φ - \sqrt[]{4 + {tg}^{2} φ}}{2 cos^{2} φ} . \end{matrix}

Fritz József (Mosonmagyaróvár, Kossuth L. g. IV. o. t.)