Kezdőlap


Feladat:	99. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Hunyadi K. , Ignácz Pál , Máté Attila , Náray Szabó Gábor , Perjés Zoltán , Rába Ferenc , Veress Árpád
Füzet:	1961/április, 181 - 182. oldal		PDF \| MathML
Témakör(ök):	Coriolis-erő, Munkatétel, Egyéb síkmozgás, Feladat
Hivatkozás(ok):	Feladatok: 1960/november: 99. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a forgó korongot és a sugárirányban fallal terelt testet egy rendszernek, és vizsgáljuk meg az energiaváltozásokat. Miközben a súrlódásmentesen egyenletes sebességgel csúszó test $r$ sugárról $R$ sugárra megy, a rendszer energiája nő, a külső erő munkája biztosítja a szögsebesség állandóságát.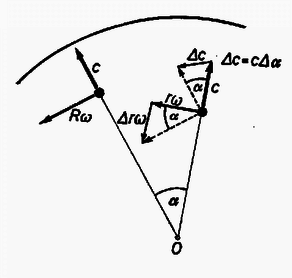

Ugyanekkor a fellépő centrifugális erő is végez munkát, hiszen irányában történik a test mozgása. Mi azonban kívülről egyenletes sebességre fogjuk vissza a testet, így a centrifugális erő munkája nem a test kinetikus energiáját növeli, hanem a külső rendszeren végez munkát (kezünkön, vagy pl. felhalmozódhat egy megfelelő mechanikus berendezésben). Így az energiamérleg a következőképpen alakul: a rendszer energiája a test sebességnövekedésével mozgási energiatöbblethez jutott, viszont potenciális energiája csökkent (a centrifugális erő munkát végzett a fékező kezünkön, közben a test kisebb potenciálú helyre került), ugyanakkor a külső rendszer energiája csökkent a szögsebességtartásra fordított forgató munkával és nőtt a centrifugális erő által végzett munkával. Így a haladó test mozgási energiájának növekedése egyenlő a külső rendszer energiájának csökkenésével, vagyis:

\begin{matrix} Δ E_{m} = L_{külső} - L_{c f}, ahol L_{külső} = L_{-cor}, \end{matrix}

azaz

\begin{matrix} \frac{1}{2} m v_{2}^{2} - \frac{1}{2} m v_{1}^{2} + m \frac{R + r}{2} ω^{2} (R - r) = m a \frac{R + r}{2} ω t | : \frac{R + r}{2} m . \end{matrix}

Figyelembe vettük, hogy a centrifugális erő egyenletesen növekszik, így átlagértékkel kell számolnunk, hasonlóképpen azt is, hogy a Coriolis-erő átlagos útja a két szélső helyzethez tartozó ívhossz számtani közepe.

\begin{matrix} (R - r) ω^{2} + (R - r) ω^{2} = a ω t, \\ 2 (R - r) ω^{2} = a ω t, innen a = \frac{2 (R - r)}{t} ω = 2 c ω . \end{matrix}

(Több dolgozat alapján.)

b) kérdés;

I. megoldás: A gyorsulás definíciója:

a = \frac{v_{t} - v_{0}}{t}

, ahol a betűk jelentése ismert.

\vec{v} = \vec{c} + \vec{r \cdot ω}

, ahol

\vec{c} ⊥ \vec{r \cdot ω}

Δ \vec{v} = \vec{c} + Δ \vec{r \cdot ω}, | Δ \vec{c} | = c \cdot a

| Δ \vec{r \cdot ω} | = \sqrt[]{r^{2} \cdot ω^{2} + R^{2} ω^{2} - 2 r R ω^{2} cos α}

(a cosinus-tétel alapján).

a = \frac{Δ v}{Δ t}

, ha

Δ \to 0

, akkor

α \to 0

cos α \to 1

, és

| Δ \vec{r \cdot ω} | \to \sqrt[]{{(R w - r \cdot ω)}^{2}} = R ω - r ω

. Így a sebesség teljes megváltozása

Δ v = c a + (R ω - r ω) = c \cdot ω t + (R - r) ω

a = \frac{Δ v}{Δ t} = c ω + \frac{R - r}{t} ω = c ω + c ω = 2 c ω

Máté Attila (Szeged, Dózsa Gy. ált. isk. VIII. o. t.) dolgozata alapján

II. megoldás: Adva van egy

v = r \cdot ω

sebességgel forgó korong. Ezen egy sugárirányban lefektetett sínen mozog egyenletesen

c

sebességgel egy

m

tömegű kocsi. A kifelé mozgás következtében a kocsi kerületi sebessége

t

idő alatt zérusról

v_{1} = r_{1} ω

értékre nő, tehát a kocsi kerületi gyorsulása

a_{k} = r_{1} ω / t = v \cdot ω

. A korong forgása következtében van a kocsinak a haladás irányára merőleges gyorsulása is, amelynek hatására irányát változtatja. (Ez centripetális gyorsulás.) Ennek értéke

a_{n} = v \cdot ω

, hiszen a sugárirányú sebességvektor irányváltozásából ugyanúgy vezethető le, mint a centripetális gyorsulás általában. (Az irányváltozás szöge éppen

t

!) A kétféle gyorsulás megegyezik, tehát algebrailag összegezhetők. Az ennek hatására ébredő tehetetlenségi erő a Coriolis-erő, és a megfelelő gyorsulás a Coriolis gyorsulás (az előzővel ellentétes).

\begin{matrix} a_{cor} = a_{n} + a_{k} = ω v + v ω = 2 v ω . \end{matrix}

Veress Árpád (Bp., József Attila g. IV. o. t.)