Kezdőlap


Feladat:	81. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bor Edit , Bresztyenszky Júlia , Lipcsey Zsolt , Rácz László , Szidarovszky Ferenc
Füzet:	1961/január, 43 - 44. oldal		PDF \| MathML
Témakör(ök):	Csúszó súrlódás, Egyenletes mozgás (Egyenes vonalú mozgások), Teljesítmény, Feladat
Hivatkozás(ok):	Feladatok: 1960/október: 81. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha a test a lap mellett nem csúszna, akkor a szalaghoz viszonyítva $v_{1}$ sebességgel mozogna. $v_{1}$ és $v$ ellentétes irányú, de egyenlő nagyságú, ezért $v_{1} = 2 m/sec$ . Jelölje a testnek a lap mentén $A$ -tól $B$ felé mutató keresett sebességét $\vec{c_{1}}$ . Ha tehát figyelembe vesszük a testnek a lap melletti csúszását is, akkor a testnek a szalaghoz viszonyított $\vec{u_{1}}$ sebessége a $\vec{v_{1}}$ és $\vec{c_{1}}$ sebességek eredője lesz.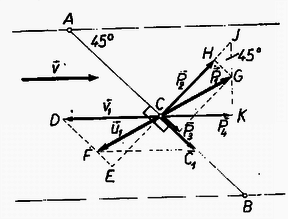

A szalag a hozzá viszonyítva

u_{1}

sebességgel mozgó test alsó lapjára az

u_{1}

-gyel ellentétes irányú

P_{1} = μ \cdot 10 kp = 0, 2 \cdot 10 k p = 2 kp

súrlódási erőt gyakorol.

P_{1}

A B

-re merőleges és

A B

irányába eső összetevőkre bontható

(P_{2}

P_{3})

. Mivel a test

B

felé állandó sebességgel csúszik, azért a

P_{3}

éppen akkora, mint a

P_{2}

nyomóerő következtében a test oldallapján fellépő

μ_{2} \cdot P_{2} = 0, 1 \cdot P_{2}

surlódási erő. Pythagoras tétele szerint

P_{1}^{2} = P_{2}^{2} + P_{3}^{2}

4 {kp}^{2} = P_{2}^{2} + 0, 01 P_{2}^{2};