Kezdőlap


Feladat:	65. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Németh István , Rozváczy Judit , Vesztergombi György
Füzet:	1960/december, 230 - 231. oldal		PDF \| MathML
Témakör(ök):	Súlypont (tömegközéppont) meghatározása, Feladat
Hivatkozás(ok):	Feladatok: 1960/május: 65. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A három betűből álló rendszer súlypontja akkor esik a középen levő I betű középpontjába, ha erre a pontra nézve a két szélső betű forgatónyomatéka egyenlő. Minthogy a V és Z betűk külön-külön vett súlypontja a téglalap felezővonalába esik, így az erőkarok egyenlőek. Ebből következik, hogy V és Z betűk tömege is egyenlő kell, hogy legyen. Ha a téglalapok alapja egységnyi, függőleges oldala pedig $n$ hosszúságú, akkor a betűk hossza:

\begin{matrix} V = 2 \sqrt[]{n^{2} + 0, 5^{2}}, Z = 2 + \sqrt[]{n^{2} + 1} . \end{matrix}

A betűk súlya arányos a vonalak hosszával. A két hosszúságot egyenlővé tesszük:

\begin{matrix} 2 \sqrt[]{n^{2} + 0, 5^{2}} = 2 + \sqrt[]{n^{2} + 1}; \end{matrix}

a megoldás

\begin{matrix} n = \frac{2}{3} \sqrt[]{10.} \end{matrix}

Ha a második kérdést úgy fogjuk fel, hogy

n

mely értékénél eshet az

5

betűből álló rendszer súlypontja a Z betű függőleges középvonalába, akkor a megoldásnál a V és T betű vonalainak hosszát kell egyenlővé tenni:

\begin{matrix} 2 \sqrt[]{n^{2} + 0, 5^{2}} = 1 + n . \end{matrix}

Ennek megoldása

\begin{matrix} n = \frac{2}{3} \end{matrix}

Rozváczy Judit (Bp., I. Szilágyi E. g. II. o. t.)

Megjegyzések. A második kérdés fogalmazása félreértésre adott alkalmat. Ez a kérdés helyesen így szól: mikor esik a VIZIT szó súlypontja a Z betű függőleges középvonalába? (A pontozásnál ebből nem származott senkire sem hátrány). Az is kérdezhető, mikor esik a súlypont a Z-betű vonalába. Erre a válasz az: csak akkor lehetséges, ha a betűk téglalapjait egymásba csúsztatjuk, de a feladat ekkor is megoldható.

(Németh István Bp., Bolyai gimn., Vesztergombi György Bp., Piarista gimn.)

Ha grafikusan ábrázoljuk V, Z és T betűk vonalhosszát, mint

n

függvényét, akkor jó áttekintést kapunk.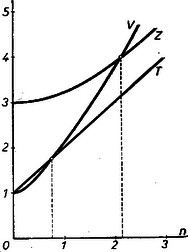

A hiperbolák metszéspontja adna a VIZ súlypontjára a választ. A VIZIT esetében

n = 0

is megoldás. A ZIZIT szó esetében nincs megoldás.