Kezdőlap


Feladat:	56. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Góth László , Kugler Emese , Mladek Ferenc , Rozváczy Judit , Vermes Miklós
Füzet:	1960/november, 178 - 179. oldal		PDF \| MathML
Témakör(ök):	Arkhimédész törvénye, Egyéb párhuzamos erők eredője, Úszás-stabilitás, Feladat
Hivatkozás(ok):	Feladatok: 1960/április: 56. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A gerendára három erő hat: A gerenda súlypontjában függőlegesen lefelé a súlyereje ( $G$ ), a kiszorított víz súlypontjában a felhajtóerő függőlegesen felfelé ( $F$ ), és a kötél húzóereje ( $P$ ). Az egyensúly feltétele: az erők összege, valamint a forgatónyomaték összege legyen zérus. A három erő közül $G$ és $F$ függőleges, tehát $P$ is az. Ezért függőleges a kötél.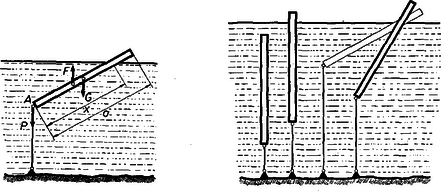

A gerenda keresztmetszete legyen

q

, akkor

G = q a γ

és

F = g x γ_{0}

, ahol

a

a gerenda hossza,

x

a vízbe merülő rész hossza.

G

a gerenda felezőpontjában,

F

a bemerült rész felezőpontjában hat. (Itt kihasználtuk azt, hogy a gerenda vékony.) A forgatónyomatékokat az

A

pontra írjuk fel, a karok helyett a velük arányos hosszakat véve:

\begin{matrix} (q x γ_{0} \cdot \frac{x}{2} = (q a γ) \cdot \frac{a}{2} amiből \frac{x^{2}}{a^{2}} = \frac{γ}{γ_{0}}, tehát \\ \frac{x}{a} = \sqrt[]{\frac{γ}{γ_{0}}}; esetünkben \frac{x}{a} = \sqrt[]{0, 64} = 0, 8. \end{matrix}

A vízbe merülő rész tehát az egész hosszúság

80 %

-a.

Kugler Emese (Nagykanizsa, Landler g. III. o. t.) és

Rozváczy Judit (Bp., Szilágyi E. g. II. o. t.)

megoldásai alapján.

Megjegyzés: Ha egész mélyről indulunk ki és először rövid kötélre kötjük a pálcát, azután a kötelet mindig hosszabbítjuk, a pálca eleinte függőlegesen emelkedik. Ha a vége kiáll a vízből, még mindig függőleges mindaddig, amíg

\begin{matrix} x = \sqrt[]{\frac{γ}{γ_{0}}} \cdot a . \end{matrix}

Megvizsgálandó a stabilitás kérdése. Meg lehet mutatni, hogy abban az esetben, amikor

a > x > a \sqrt[]{\frac{γ}{γ_{0}}}

, a rúdnak a függőlegesből való kimozdulása olyan forgatónyomatékot ad, amely visszaviszi a rudat függőleges helyzetébe.

h < a \cdot \sqrt[]{\frac{γ}{γ_{0}}}

esetén két egyensúlyi helyzet lehetséges. A fenti ferde helyzeten kívül ugyanis a gerenda függőleges helyzetben is egyensúlyban van. (Teljesülnek az egyensúly feltételei.) Ez azonban labilis egyensúlyi helyzet, a gerenda bármely kis elmozdítása esetén a súlyerő forgatónyomatéka,

F_{1}

nagyobb mint

F_{2}

, (lásd a diagramot

a = 0

-nál), tehát a gerendát kibillenti a ferde egyensúlyi helyzetnek megfelelő

α

szögr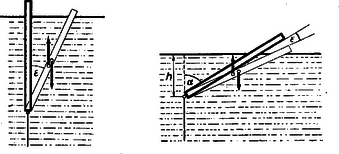e.

Ha a ferdén úszó esetről van szó, amikor

x = a \sqrt[]{\frac{γ}{γ_{0}}}

és

ε

-nal növekszik a függőlegessel alkotott

α

szög, a lefelé vivő forgatónyomaték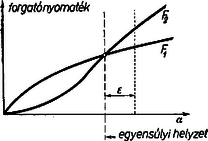

\begin{matrix} F_{1} = \frac{γ a^{2} q}{2} \cdot sin (α + γ), \end{matrix}

a visszavivő forgatónyomaték

\begin{matrix} F_{2} = \frac{h^{2}}{2 cos^{2} (α + ε)} \cdot q \cdot γ_{0} sin (α + ε) . \end{matrix}

(

q

a rúd keresztmetszet területe,

h

a rúd végének a mélysége a víz szintje alatt). A forgatónyomatékok szögtől való függését ábránk tünteti fel.

A két forgatónyomaték görbéjének metszéspontja adja meg az egyensúly helyzetét. Látható, hogy a szöget növelve a visszavivő forgatónyomaték a nagyobb, tehát a rúd visszatér egyensúlyi helyzetébe; így az egyensúly stabilis. Amikor a rúd vízszintesen a víz felszínére kerül, más körülmények határozzák meg helyzetét.

Vermes Miklós