Kezdőlap


Feladat:	47. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Békési József , Farkas Ferenc , Góth László , Grad János , Horváth Sándor , Mezei Ferenc , Molnár Emil , Várady Gábor , Varsányi István
Füzet:	1960/október, 95 - 96. oldal		PDF \| MathML
Témakör(ök):	Arkhimédész törvénye, Izotermikus állapotváltozás (Boyle--Mariotte-törvény), Feladat
Hivatkozás(ok):	Feladatok: 1960/február: 47. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Alkalmazzuk Archimedes törvényét a pohár és a benne szorult levegő együttesére. Egyensúlyi helyzetben a pohár súlya a kiszorított higany súlyával és a dinamométer 20,028 $π$ pond erejével tart egyensúlyt (a bennszorult levegő súlyától, a levegő felhajtóerejétől és egyéb zavaró tényezőktől eltekintünk).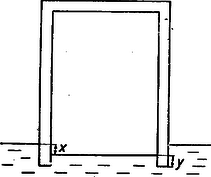

A pohár súlya

13, 6 (3, 2^{2} \cdot π \cdot 10, 2 - 3^{2} \cdot π \cdot 10) pond=36,12 pond

,
a kiszorított higanymennyiség súlya

13, 6 [3, 2^{2} π x + (3, 2^{2} - 3^{2}) π y] = 139, 264 π x + 16, 864 π y

pondokban. Tehát

\begin{matrix} 36, 12 π = 20, 028 π + 139, 264 π x + 16, 864 π y . \end{matrix}

(1)

A lemerülés után a higany addig hatol a pohárba, amíg a higany-szintkülönbségből eredő nyomás meg nem egyezik a pohárba zárt levegő túlnyomásával; azaz Boyle-Mariotte törvény alapján ‐ figyelembevéve, hogy a normális légnyomás 76 cm-es higanyoszlop nyomásának felel meg:

\begin{matrix} \frac{10 \cdot 76}{10 - y} = x + 76, innen 76 y = x (10 - y) . \end{matrix}

(2)

(1)-ből összevonás, 4-gyel való egyszerűsítés után

\begin{matrix} x = \frac{4, 023 - 4, 216 y}{34, 816} . \end{matrix}

Ezt (1)-be helyettesítve a

4, 216 y^{2} - 2692, 199 y + 40, 23 = 0

másodfokú egyenletet nyerjük, melynek fizikailag szóbajöhető gyöke

y \approx 0, 015

. A pohárba zárt levegőoszlop magassága tehát 9,985 cm.

Molnár Emil (Györ, Révai M. g. III. o. t.)

Megjegyzés. A megoldásban szereplő (1) egyenlethez eljuthatunk azon meggondolás alapján is, hogy a pohár súlyerejét a zsinórban ható erő, a pohár peremén működő felhajtóerő, valamint a pohár belső körlapján ható, a bennszorult levegő túlnyomásából eredő nyomó erő egyenlíti ki.

Horváth Sándor (Bp., II. Rákóczi F. g. IV. o. t.)