Kezdőlap


Feladat:	29. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Mezey Ferenc , Nagy Béla
Füzet:	1960/május, 194 - 196. oldal		PDF \| MathML
Témakör(ök):	Tökéletesen rugalmas ütközések, Hajítások, Feladat
Hivatkozás(ok):	Feladatok: 1959/december: 29. fizika feladat

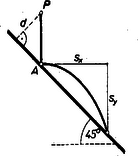
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A lejtő eléréséig a golyó $s = d \sqrt[]{2}$ úton szabadon esik. $A$ -ban sebessége $v = \sqrt[]{2 g s} = \sqrt[]{2 g d \sqrt[]{2}}$ . Mivel az ütközés rugalmas, és $45^{\circ}$ -os beesés alatt történik, a golyó ugyanezen $v$ nagyságú, de vízszintes irányú sebességgel hagyja el $A$ -t. Ekkor már a vízszintes hajítás pályáján mozog, így elmozdulásának vízszintes összetevője $s_{x} = v t$ , a függőleges összetevő pedig $s_{y} = \frac{g}{2} \cdot t^{2}$ .

Akkor ér ismét a lejtőre, amikor

s_{x} = s_{y}

, vagyis

v t = \frac{g}{2} \cdot t^{2}

, amiből

t = \frac{2 v}{g}

. Ekkor az elmozdulás vízszintes komponense

s_{x} = \frac{2 v^{2}}{g}

, ahonnan

A B = s_{x} \sqrt[]{2} = \frac{2 \cdot 2 g d \sqrt[]{2} \cdot \sqrt[]{2}}{g} = 8 d

Nagy Béla (Nyíregyháza, Vasvári P. gimn. IV. o. t.)

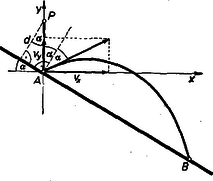
II. megoldás: Vizsgálhatjuk a feladatot tetszőleges

α

szögű lejtő esetén. A golyó pályájának síkjában vegyünk fel egy derékszögű koordinátarendszert az ábrán látható módon.

Ebben az

A B

egyenes egyenlete:

y = - tgα\cdotx

. A golyó szabadesés útján szerzett sebessége az

A

pontban

v = \sqrt[]{2 \cdot A P \cdot g} = \sqrt[]{\frac{2}{cos α} d g}

. Az ütközés után ferde (ill. vízszintes) hajítás jön létre

v

nagyságú kezdősebességgel, iránya a rugalmas ütközés törvényei szerint a függőlegessel

2 α

szöget alkot. Tehát a kezdősebesség vízszintes irányú komponense

v_{x} = v sin 2 α

, függőleges irányú komponense

v_{y} = v cos 2 α

(

α > 45^{\circ}

esetén is előjel szerint helyesek ezen értékek). Az ütközés után

t

idővel a golyó helyének koordinátái

\begin{matrix} x = v_{x} t = v t sin 2 α, \end{matrix}

(1)

\begin{matrix} y = v_{y} t - \frac{g}{2} t^{2} = v t cos 2 α - \frac{g}{2} t^{2} . \end{matrix}

(2)

(1)-ből

t = \frac{x}{v sin 2 α}

, továbbá

v = \sqrt[]{\frac{2}{cos α} dg}

felhasználásával a pálya egyenlete:

\begin{matrix} y & = \frac{v cos 2 α}{v sin 2 α} x - \frac{g}{2 \cdot \frac{2}{cos α} d g {sin}^{2} 2 α} \cdot x^{2} = - x^{2} \frac{1}{16 d {sin}^{2} α cos α} + x ctg 2α. \end{matrix}

Így meghatározhatjuk a pálya és az

A B

egyenes metszéspontját:

\begin{matrix} - tg α \cdot x = - x^{2} \frac{1}{16 d {sin}^{2} α cos α} + x ctg 2 α, ahonnan (x \neq 0) \end{matrix}

\begin{matrix} x = 16 d {sin}^{2} α cos α (tg α + ctg 2 α) = 16 d \frac{{tg}^{2} α}{1 + {tg}^{2} α} cos α (tg α + \frac{1 - {tg}^{2}α}{2 tg α}) = 8 d cos α tg α . \end{matrix}

Tehát

A B = \frac{x}{cos α} = 8 d tg α

, ezért

α = 45^{\circ}

esetén

A B = 8 d

Mezey Ferenc (Budapest, II. Rákóczi F. gimn. IV. o. t.)

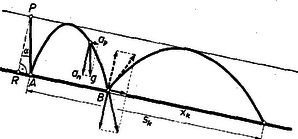
III. megoldás: Bontsuk föl a golyó gyorsulás- és sebességvektorát a lejtőre merőleges és azzal párhuzamos összetevőre. Tetszőleges

α

hajlásszöge lejtő esetén a gyorsulás normális irányú komponense

a_{n} = g cos α

, a lejtő síkjával párhuzamos komponense

a_{p} = g sin α

(az ütközési pillanatok kivételével). Ütközéskor a sebesség lejtővel párhuzamos irányú komponense nem változik, arra merőleges összetevője pedig csupán irányt változtat. Ezért a golyónak a lejtővel párhuzamos elmozdulás-komponense az indítástól számított

t

idő múlva

\begin{matrix} s_{p} = a_{p} t = g t sin α . \end{matrix}

A lejtőre merőleges irányú komponenst vizsgálva: először a test

a_{n} = g cos α

gyorsulással halad

d

távolságon a lejtő felé, így a lejtőt

t_{0} = \sqrt[]{\frac{2 d}{a_{n}}} = \sqrt[]{\frac{2 d}{g cos α}}

idő alatt éri el. Mivel a gyorsulás változatlan és a sebesség csak irányt változtat, éppen

t_{0}

idő alatt teszi meg az utat a lejtőtől a holtpontig, mely a lejtőtől nyilván

d

távolságra van. Így az első ütközés

t_{0}

időpillanatban, a második

t_{0} + 2 t_{0} = 3 t_{0}

, a

k

-adik

t_{0} + 2 t_{0} (k - 1) = (2 k - 1) t_{0}

időpillanatban következik be az indulástól számítva. Ezért a

k

-adik pattanási helynek

R

-től való távolsága

\begin{matrix} s_{k} = \frac{a_{p}}{2} {[(2 k - 1) t_{0}]}^{2} = \frac{g sin α}{2} {(2 k - 1)}^{2} \frac{2 d}{g cos α} = {(2 k - 1)}^{2} d tgα, \end{matrix}

amiből a

k

-adik és a

(k + 1)

-edik pattanási hely távolsága

\begin{matrix} x_{k} {[2 (k + 1) - 1]}^{2} d tg α - {(2 k - 1)}^{2} d tg α = [{(2 k + 1)}^{2} - {(2 k - 1)}^{2}] d tg α = 8 k tg α \cdot d . \end{matrix}

k = 1

α = 45^{\circ}

helyettesítéssel a kívánt eredményt kapjuk.

Mezey Ferenc (Budapest, II. Rákóczi F. gimn. IV. o. t.)