Kezdőlap


Feladat:	1937. évi Eötvös (később Kürschák) matematikaverseny 2. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Czeizler Gy. , Holzer Pál , Komlós János , Krisztonosich Jenő , Sándor Gyula , Schreiber Béla , Vajnai I. , Weisz Alfréd
Füzet:	1938/január, 130 - 131. oldal		PDF \| MathML
Témakör(ök):	Gömb és részei, Körülírt kör középpontja, Térgeometriai bizonyítások, Körérintők, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1937/november: 1937. évi Eötvös (később Kürschák) matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Előrebocsátjuk, hogy a kör érintője a kör síkjában fekszik. Ha két érintkező kör nem fekszik egy síkban, akkor közös érintőjük a két kör síkjának metszési vonala.
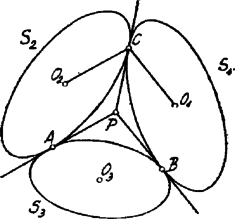
a) Ha a három kör közül kettő, $k_{1}$ és $k_{2}$ egy síkban $(S)$ fekszik, akkor a harmadik kör, $k_{3}$ is az $S$ síkban fekszik.
Ugyanis $k_{1}$ és $k_{3}$ közös érintője az $S$ , $k_{2}$ és $k_{3}$ közös érintője is az $S$ síkban fekszik. Ezen két érintő meghatározza a $k_{3}$ síkját, azaz $S$ -t.
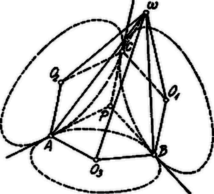
b) Ha két kör nem fekszik egy síkban, akkor a harmadik sem feküdhetik az előbbiek egyikével sem egy síkban, ha a három érintkezési pont különböző: a három kör, $k_{1}$ , $k_{2}$ , $k_{3}$ ( $O_{1}$ , $O_{2}$ , $O_{3}$ középpontokkal) a különböző $S_{1}$ , $S_{2}$ , $S_{3}$ síkokban fekszik. Két kör közös érintője síkjuknak metszésvonala; a három közös érintő egy triéder élei. A triéder csúcsa legyen $P$ .

k_{1}

és

k_{2}

körök érintési pontja legyen

C

, a

k_{2}

és

k_{3}

köröké

A

, a

k_{3}

és

k_{1}

köröké

B

. Az

O_{1} C

és

O_{2} C

sugarak meghatároznak egy

Σ_{3}

síkot, mely a

P C

közös érintőre merőleges.^{$^{*}$} Ha a

Σ_{3}

síkban

O_{1} C

-re az

O_{1}

-ben és

O_{2} C

-re az

O_{2}

-ben merőlegest állítunk, ezek egy

ω

pontban metszik egymást. Már most

O_{1} ω ⊥ S_{1}

O_{2} ω ⊥ S_{2}

,^{$^{*}$} tehát

ω

k_{1}

és

k_{2}

körök minden pontjától egyenlő távolságban van:

ω

oly gömb középpontja, melynek gömbi körei

k_{1}

és

k_{2}

. A gömb sugara

ω C = ω B = ω A = R

Már most az

O_{1} B O_{3} \equiv Σ_{2}

síkban az

O_{3}

pontban,

S_{3}

-ra merőleges egyenesnek metszenie kell az

O_{1} ω

egyenest; az

O_{2} A O_{3} \equiv Σ_{1}

síkban az

O_{3}

pontban,

S_{3}

-ra merőleges egyenesnek metszenie kell az

O_{2} ω

egyenest. Ez csak úgy lehetséges, ha

O_{1} ω

-t és

O_{2} ω

-t éppen az

ω

-ban metszi,^{$^{*}$} azaz

ω

k_{3}

kör minden pontjától

ω B = ω A = R

távolságban van. Eszerint

k_{1}

k_{2}

k_{3}

körök az

(ω, R)

gömbön feküsznek. Az

ω

Σ_{1}

Σ_{2}

Σ_{3}

síkoknak közös pontja; oly triéder csúcsa, melynek élei

ω O_{1}

ω O_{2}

ω O_{3}

.
c) Ha

P

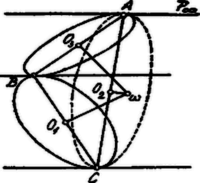
a végtelenben van, akkor a triéder éleiként szereplő közös érintők párhuzamosak (egy hasábos tér élei).

Egy kör két érintője akkor párhuzamos, ha az érintési pontok egy átmérő végpontjai. Jelen esetben tehát az

A B C △

oldalai a

k_{1}

k_{2}

k_{3}

körök átmérői; a

Σ_{1}

Σ_{2}

Σ_{3}

síkok összeesnek az

A B C △

síkjával, tehát

ω

is ezen síkban van és nem más, mint az

A B C △

köré írt kör középpontja.

Weisz A.

^{$^{*}$}Ugyanis

O_{1} C ⊥ P C

és

O_{2} C ⊥ P C

^{$^{*}$} $O_{1} ω ⊥ S_{1}$ , mert: $Σ_{3} ⊥ P C$ , tehát $P C$ merőleges a $Σ_{3}$ síkban fekvő bármely egyenesre; így $O_{1} ω ⊥ P C$ és $O_{1} ω ⊥ O_{1} C$ . Hasonlóan következik: $O_{2} ω ⊥ S_{2}$ .

^{$^{*}$}Ha az $e_{3}$ egyenes, mely nem fekszik az $e_{1}$ és $e_{2}$ egymást metsző egyenesek síkjában, metszi úgy az $e_{1}$ -et, mint az $e_{2}$ -t, akkor $e_{3}$ az $e_{1}$ és $e_{2}$ metszéspontján megy keresztül.