Feladat: 1930. évi Eötvös (később Kürschák) matematikaverseny 3. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Albrecht J. ,  Alpár L. ,  Balassa Gy. ,  Baranyai K. ,  Bársony I. ,  Bársony Stefánia ,  Barta F. ,  Budó Á. ,  Busztin Anna ,  Csoma Zs. ,  Deckner G. ,  Deutsch I. ,  Faragó S. ,  Fejér Gy. ,  Gajzágó E. ,  Gohn E. ,  Jónás J. ,  Kerékgyártó Jenő ,  Klein Béla ,  Kmoschek P. ,  Kövesdi D. ,  Lévay K. ,  Nagymihály L. ,  Nánássy Éva ,  Nay A. ,  Pólya J. ,  Salamin P. ,  Scholcz G. ,  Sebők Gy. ,  Serényi G. ,  Simon Á. ,  Singer Gy. ,  Spira E. ,  Szabó F. ,  Székely I. ,  Váradi L. ,  Vida L. ,  Weiszfeld E. ,  Zsemlye B. ,  Zsoldos Pál 
Füzet: 1931/január, 134 - 136. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek nevezetes tételei, Körülírt kör, Körülírt kör középpontja, Geometriai egyenlőtlenségek, Háromszög-egyenlőtlenség alkalmazásai, Derékszögű háromszögek geometriája, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1930/november: 1930. évi Eötvös (később Kürschák) matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás.1 Ha az ABCΔ hegyesszögű, akkor a körülírt kör O középpontja a háromszög belsejében van.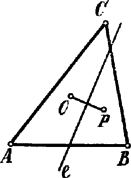

 

 

Húzzuk meg az OP távolságot merőlegesen felező e egyenest. Ezen egyenes, minthogy az OP távolság felezőpontja is a háromszögön belül van, ezt kettészeli. A háromszög csúcsai közül mindig lesz egy, amely az O-val és egy, amely a P-vel, az e egyenes ugyanazon oldalán van. Az előbbinek P-től való távolsága >R, az utóbbié <R.
 

II. Megoldás. A háromszög belsejében felvett P pont az AOB, BOC, COA háromszögek egyikének belsejében (vagy az AO, BO, CO határvonalak egyikén) fekszik; legyen pl.az AOBΔ belsejében.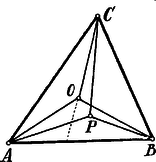
 

 

Az AOBΔ belsejében felvett P pontra nézve áll:
AP+BP<AO+BO=2R;(1)
kell tehát, hogy az AP, BP távolságok egyike R-nél kisebb legyen.
A P pont az AOCΔ-re (vagy a BOCΔ-re) olyan helyzetű, hogy az AO+CO törtvonal az AP+CP (vagy a BO+CO a BP+CP) törtvonalon belül esik, tehát
AP+CP>AO+CO=2R;(2)
kell tehát, hogy az AP, CP távolságuk valamelyike az R-nél nagyobb legyen.
Ha a P pont az AOBΔ belsejében a CO folytatásába esik, akkor az (1) fennáll és CP>CO=R.
Ha a P pont a BO-ra esik, akkor BP<BO=R; a (2) érvényben marad.
 

Kerékgyártó Jenő (Bolyai r. VII. o. Bp. V.).
 

III. Megoldás. Ha az O pontot összekötjük a háromszög A, B, C csúcsaival és O-ból merőlegeseket állítunk a háromszög oldalaira, akkor a P pont az így keletkező hat derékszögű háromszög egyikéken (vagy határán) lesz. Ezen derékszögű háromszög átfogója OX=R, ahol X az A, B, C csúcsok egyike; tehát 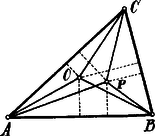PX<R.1
 

 

Ha P pontot kötjük össze a csúcsokkal és P-ből merőlegeseket állítunk a háromszög oldalaira, akkor az O pont az így keletkező hat derékszögű háromszög egyikében (vagy határán) lesz. Ezen derékszögű háromszög átfogója PY, ahol Y az A, B, C csúcsok egyike tehát PY>OY=R.
 

Zsoldos Pál (Érseki rg. VII. o. Bp. II.).

 

 

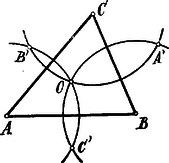IV. Megoldás. Az A, B, C csúcsokból, mint középpontokból az AO, BO, CO sugarakkal rajzolt körök közül kettő-kettő ‐ a háromszögön belül az O pontban és még a háromszögön kívül metszi egymást2 (az O pontnak a háromszög egy-egy oldalára vonatkozó szimmetrikus pontjában*), tehát a három körnek; közös területrésze nem lehet.
Másrészt egyik kör sem foglalhatja magában a másik két kör közös részét. A háromszög belsejében felvett P pont legalább ezen körök egyikén belül és egyikén kívül fekszik; ezért az AP, BP, CP távolságok egyike <R és egyike >B.
 

Klein Béla (Kölcsey Ferenc rg. VIII. o, Bp. VI.)
1Ezen megoldás Fejér Lipót egyetemi tanár úrtól származik.

1L. KURSCHÁK: Mat. Versenytételek, XIV .

2Ugyanis R bármely oldal felénél nagyobb!

*Helyesebben: az O pontnak valamely oldalra vonatkozó szimmetrikus pontját az illető oldal, a vele szemben fekvő csúcstól elválasztja. Tompaszögű háromszög esetében ez nem áll a tompaszöggel szemben fekvő oldalra! A tompaszög csúcsából R sugárral rajzolt kör magában foglalja a másik két kör közös részét is; ezen részben fekvő P pontnak mindegyik csúcstól ezen való távolsága 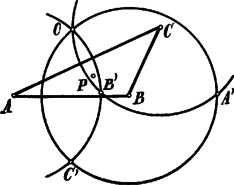<R.

 

 

Derékszögű háromszög esetében O az átfogó felezőpontja; most O összeesik az átfogóra vonatkozó szimmetrikus pontjával. Ha az átfogó végpontjai A és B, az AO és BO sugarú körök az O pontban érintkeznek, a CO sugarú kör az előbbiek mindegyikét az O ponton kívül még egy pontban metszi. A tétel ebben az esetben már érvényes.