Kezdőlap


Feladat:	1304. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Faragó K. , Kovács Ervin , Steiner Gábor
Füzet:	1939/január, 120 - 121. oldal		PDF \| MathML
Témakör(ök):	Mértani helyek, Gyakorlat, Magasságvonal, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 1938/november: 1304. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $O A B △$ magasságainak talppontjai legyenek ábránk szerint $M$ , $N$ , $P$ . Az $O$ pontból bocsátott magasság talppontja az $e$ egyenesen mindig 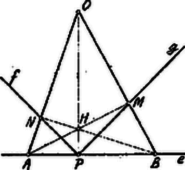$P$ .

Jelölje

H

a magassági pontot. Az

A P H N

négyszög az

A H

átmérő fölött írt körbe írt háromszög. Ezért

H P N ∢ = H A N ∢

, t. i. a

\hat{H N}

ívhez tartozó kerületi szögek. Azonban az

A O M

derékszögű háromszögben

H A N ∢ = 90^{\circ} - A O B ∢

és így

H P N ∢ = 90^{\circ} - A O B ∢

.
Hasonlóan

H P M ∢ = 90^{\circ} - A O B ∢

Minthogy

P

szilárd pont, az

M

és

N

O P

-re szimmetrikus helyzetű

f

és

g

egyeneseken feküsznek, melyek

O P

-vel meghatározott szöget zárnak he.
Feltételeztük, hogy

A O B

hegyes szög. Ha azonban

A O B

tompa szög, hasonló gondolatmenettel azt találjuk, hogy

\begin{matrix} A P N ∢ = H P M ∢ = A O B ∢ - 90^{\circ} . \end{matrix}

Ha pedig

A O B ∢ = 90^{\circ}

, akkor az

M

és

N

pontok mindig az

O

pontba esnek.
Ha

A O B

nem derékszög, akkor a szöget bezáró egyenesek által meghatározott

A B

szelet az

e

egyenesen feküdhetik a hegyes szög vagy mellékszögének szárai között. Ha a hegyes szög

ω

, mellékszöge

180^{\circ} - ω

. Azonban

(180^{\circ} - ω) - 90^{\circ} = 90^{\circ} - ω

. Tehát a

H P N

H P M

szögek nagysága mindig ugyanaz marad.

O A

felvehet minden irányt;

N

leírja az egész

f

egyenest, hasonlóan

M

az egész

g

egyenest.

Kovács Ervin (Kegyesrendi g. VI. o. Bp.).