Kezdőlap


Feladat:	1273. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Baán Sándor , Bizám György , Dénes László , Erőd Márta , Faragó Kálmán , Fonó András , Freud Géza , Frisch R. , Guttmann István , Haraszthy András , Hódi Endre , Hoffmann Tibor , Kalcsó Gyula , Kellermann Gy. , Kunstädter L. , Lipsitz Imre , Ozoróczy Gyula , Róka Ede , Steiner Iván , Szittyai Dezső , Szlovák István
Füzet:	1938/október, 34 - 35. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül háromszögekben, Mértani középtételek derékszögű háromszögekben, Gyakorlat, Pitagorasz-tétel alkalmazásai
Hivatkozás(ok):	Feladatok: 1938/május: 1273. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A szabályos $A B C △$ $B$ csúcsában a $B C$ oldalra merőlegest állítunk; legyen az $e$ . A $D A D' △$ a $D D' = 2 a$ átmérőjű körben, $A$ -nál derékszögű. Ha az $A$ csúcs vetülete $e$ -n a $H$ pont, akkor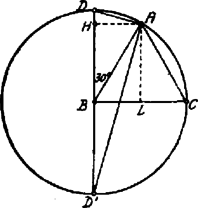

\begin{matrix} {\bar{A D}}^{2} = \bar{D D'} \cdot \bar{D H} = 2 a \cdot \bar{D H} = 2 a (D B - H B) = 2 a (a - H B) \\ {\bar{A D'}}^{2} = \bar{D D'} \cdot \bar{D' H} = 2 a \cdot \bar{D' H} = 2 a (B D' + H B) = 2 a (a + H B) . \end{matrix}

A B H △

H

-nál derékszögű;

B

-nél

30^{\circ}

-ú hegyesszöge van: ezért

A B H △ ≃ A C L △

, tehát

H B = A L = a \frac{\sqrt[]{3}}{2}

. Eszerint

\begin{matrix} {\bar{A D}}^{2} = 2 a (a - a \frac{\sqrt[]{3}}{2}) = a^{2} (2 - \sqrt[]{3}) \\ A D = a \sqrt[]{2 - \sqrt[]{3}} és A D' = a \sqrt[]{2 + \sqrt[]{3}} . \end{matrix}

Dénes László (Szent-István g. V. o. Bp. XIV.)

Jegyzet.

A D

a

sugarú körbe írt szabályos tizenkétszög oldala,

A D'

ezen sokszög egyik átlója.
Könnyen igazolható, hogy¹

\sqrt[]{2 \pm \sqrt[]{3}} = \frac{\sqrt[]{6} \pm \sqrt[]{2}}{2}

¹L. XIV. évf.(1937/11) 65. o., az 1340. feladat III.megoldásában.