Kezdőlap


Feladat:	1262. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bizám György , Freud Géza , Hajdu Á. , Hoffmann Tibor , Horváth Sándor , Klacskó Géza , Lipsitz Imre
Füzet:	1938/szeptember, 6. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül, Másodfokú (és arra visszavezethető) egyenletek, Paraméteres egyenletek, Gyakorlat, Mértani középtételek derékszögű háromszögekben
Hivatkozás(ok):	Feladatok: 1938/április: 1262. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$A B C$ a $C$ -nél derékszögű háromszög. A derékszögű háromszög befogójára vonatkozó tétel szerint: 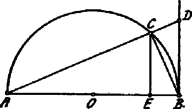${\bar{A C}}^{2} = \bar{A B} \cdot \bar{A E} = 2 R x$

Minthogy

C E ∥ D B

, írhatjuk:

C D : E B = A C : A E

. Innen

\begin{matrix} {\bar{C D}}^{2} = \frac{{\bar{E B}}^{2} \cdot {\bar{A C}}^{2}}{{C E}^{2}} = \frac{{(2 R - x)}^{2} 2 R x}{x^{2}} = \frac{{2 R (2 R - x)}^{2}}{x} \end{matrix}

Továbbá:

D B : C E = A B : A E

tehát

\begin{matrix} {\bar{D B}}^{2} = \frac{{\bar{C E}}^{2} \cdot {\bar{A B}}^{2}}{{\bar{A E}}^{2}} = \frac{x (2 R - x) 4 R^{2}}{x^{2}} = \frac{(2 R - x) 4 R^{2}}{x} \end{matrix}

Ezek alapján egyenletünk:

\begin{matrix} 2 R \cdot x + \frac{2 R {(2 R - x)}^{2}}{x} + \frac{(2 R - x) 4 R^{2}}{x} = 4 a^{2}, \end{matrix}

ill. kellő rendezés után:

\begin{matrix} f (x) \equiv R x^{2} - (3 R^{2} + a^{2}) x + 4 R^{2} = 0. \end{matrix}

Feladatunknak oly

x

érték felel meg, mely valós, pozitív és

2 R

-nél kisebb. Az

f (x) = 0

egyenlet gyökei valósak, ha

\begin{matrix} {(3 R^{2} + a^{2})}^{2} - 16 R^{4} \equiv (3 R^{2} + a^{2} + 4 R^{2}) (3 R^{2} + a^{2} - 4 R^{2}) \geq 0. \end{matrix}

Az első tényező mindig pozitív; a második sem lehet negatív. Kell tehát, hogy

a^{2} \geq R^{2}

legyen.
A gyökök szorzata:

4 R^{2}

és összege:

\frac{3 R^{2} + a^{2}}{R}

pozitív, tehát mind a két gyök pozitív.

\sqrt[]{4 R^{2}} = 2 R

a gyökök mértani középarányosa; ebből következik, hogy az egyik kisebb, a másik nagyobb

2 R

-nél, határesetben mindegyik

= 2 R

.
Eszerint a feladatnak csak egy megoldása van, hacsak

a^{2} \geq R^{2}

mégpedig

\begin{matrix} x = \frac{3 R^{2} + a^{2} - \sqrt[]{(a^{2} + 7 R^{2}) (a^{2} - R^{2})}}{2 R} . \end{matrix}

Horváth Sándor (Br. Kemény Zsigmond g. VI. o. Bp.)