Kezdőlap


Feladat:	1246. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bizám György , Fonó András , Freud Géza , Hoffmann Tibor , Horváth Sándor , Lipsitz Imre , Steiner Iván , Vizi László
Füzet:	1938/május, 274 - 275. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Paraméteres egyenletek, Trigonometriai azonosságok, Szélsőérték-feladatok differenciálszámítás nélkül, Szögfüggvények, síkgeometriai számítások, Gyakorlat
Hivatkozás(ok):	Feladatok: 1938/február: 1246. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen 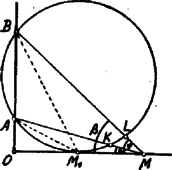$O M A ∢ = α$ , $O M B ∢ = β$ és $A M B ∢ = φ$ , Ekkor

\begin{matrix} tg φ = tg (β - α) = \frac{tg β - tg α}{1 + tg α tg β} és tg α = \frac{a}{x}, tg β = \frac{b}{x} . \end{matrix}

Helyettesítve ezeket

tg φ

értékébe:

\begin{matrix} tg φ = \frac{(b - a) x}{x^{2} + a b} . \end{matrix}

Rendezzük ezen összefüggést

x

szerint:

\begin{matrix} tg φ \cdot x^{2} - (b - a) x + a b tg φ = 0. \end{matrix}

Valós megoldást kapunk, ha

\begin{matrix} {(b - a)}^{2} - 4 a b {tg}^{2} φ ≧ 0, ill. 0 < tg φ ≦ \frac{b - a}{2 \sqrt[]{a b}} . \end{matrix}

Eszerint

tg φ

legnagyobb értéke:

tg φ_{m} = \frac{b - a}{2 \sqrt[]{a b}}

és az ehhez tartozó

x

érték:

\frac{b - a}{2 tg φ_{m}} = \sqrt[]{a b}

Steiner Iván (Toldy Ferenc g. VI. o. Bp. II.)

I. Jegyzet.

tg φ

írható:

tg φ = \frac{b - a}{x + \frac{a b}{x}}

tg φ

értéke legnagyobb, ha a nevező értéke a legkisebb. A nevező két tagjának szorzata:

a b

, állandó; a két tag összege legkisebb, ha egyenlők, ha tehát

x = \frac{a b}{x}

, ill.

x^{2} = a b

.
T. i.

{(x + \frac{a b}{x})}^{2} = {(x - \frac{a b}{x})}^{2} + 4 a b

\begin{matrix} x + \frac{a b}{x} értéke legkisebb, ha x - \frac{a b}{x} = 0, azaz x^{2} = a b . \end{matrix}

II. Jegyzet. Ezen megoldás geometriai jelentése alapján oly kört kell szerkesztenünk, mely keresztülmegy az

A

és

B

pontokon, az

O X

egyenest pedig érinti. Az

M_{1}

érintési pontra nézve

\begin{matrix} {\bar{O M}}_{1}^{2} = \bar{O A} \cdot \bar{O B} azaz x^{2} = a b . \end{matrix}

Szerkesszük meg ezen kört és vegyünk fel az

O X

egyenesen egy ‐

M_{1}

-től különböző

M

pontot. Most az

A M B ∢

a körre nézve ú. n. külső excentrikus szög, amely kisebb az

A M_{1} B

kerületi szögnél (Utóbbi mértéke az

\hat{A B}

ív fele, előbbié

\frac{1}{2} (\hat{A B} - \hat{K L})