Kezdőlap


Feladat:	1232. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Anda J. , Baka Sándor , Berényi E. , Bizám György , Böröcz Imre , Chabada György , Freud Géza , Fülöp József , György L. , Hoffmann Tibor , Horváth Sándor , Jesch Aladár , Lipsitz Imre , Martonfalvay H. , Névtelen , Schmidt Tibor , Szlovák István , Tóthfalusy M. , Vendel Z. , Vizhányó Ferenc , Vizi László
Füzet:	1938/március, 200 - 202. oldal		PDF \| MathML
Témakör(ök):	Függvényvizsgálat, Egyenesek egyenlete, Terület, felszín, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1938/január: 1232. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Az $y = - \frac{1}{2} x + 4$ egyenes az $X$ -tengelyt az $A (x = 8, y = 0)$ pontban, az $Y$ -tengelyt a $B (x = 0, y = 4)$ pontban metszi. Ezen két pont meghatározza az egyenest.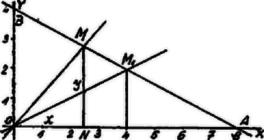
$y = m x$ az origon átmenő egyenest jelent. Ha $m = 0$ , akkor az $X$ -tengellyel esik össze. Miközben $m$ változik $0$ -tól $+ \infty$ -ig, az $y = m x$ egyenes az $O$ körül forog, az $X$ -tengelyből kiindulva, a pozitív forgási irányban, amíg az $Y$ -tengellyel esik össze. A szilárd egyenessel való metszéspontja $A$ -tól $B$ -ig mozog, tehát $M$ abscissája $8$ -tól $0$ -ig fogy.

O M N △

területe, ha

M

koordinátái

(x, y)

t = \frac{x y}{2}

. Minthogy

M

-re nézve

\begin{matrix} y = & - \frac{1}{2} x + 4, \\ t = - & \frac{1}{4} x^{2} + 2 x, \end{matrix}

ahol

x

értéke

8

-tól

0

-ig fogy. Amint látjuk, az

O M N △

területe az

x

másodfokú függvénye, mely az

x = 8

és

x = 0

helyeken zérus. Ezen függvénynek maximuma van, minthogy

x^{2}

együtthatója negatív, még pedig az

x = \frac{1}{2} O A = 4

helyen. Itt

t_{max} = 4

.
Eszerint az

O M N △

területe

0

-tól növekedik

4

-ig, azután fogy

0

-ig (a növekedéssel szimmetrikusan az

x = 4

egyenesre nézve). A terület változását egy parabola íve tünteti fel, melynek csúcspontja a görbe felső tetőpontja, főtengelye az

x = 4

egyen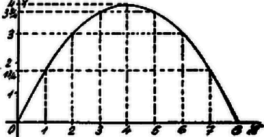es.

Részletesebb értéktáblázat:

\begin{matrix} x & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ t & 0 & ↗ & \frac{7}{4} & ↗ & 3 & ↗ & \frac{15}{4} & ↗ & 4 & ↘ & \frac{15}{4} & ↘ & 3 & ↘ & \frac{7}{4} & ↘ & 0 \end{matrix}

Jesch Aladár (Kegyesrendi g. VI. o. Bp.)

II. Megoldás. Az

O M N △

területét kifejezhetjük, mint az

m

ir. határozó függvényét. Ugyanis az

M

pont koordinátáira nézve

\begin{matrix} y = - \frac{1}{2} x + 4 és y = m x . \end{matrix}

Innen

\begin{matrix} x = \frac{8}{2 m + 1}, y = \frac{8 m}{2 m + 1} \end{matrix}

és

\begin{matrix} t = \frac{x y}{2} = \frac{32 m}{{(2 m + 1)}^{2}} ... \end{matrix}

(1)

m = 0

és

m = + \infty

mellett

t = 0

. Ha

m

változik

0

-túl

+ \infty

-ig,

t

értéke mindig pozitív. Minthogy

t

m

-nek folytonos függvénye

m

szóbanforgó értékei mellett, kell, hogy legalább egy legnagyobb értéke legyen. Hogy ezt megállapíthassuk, vizsgáljuk meg, hogy a

\begin{matrix} t = \frac{32 m}{{(2 m + 1)}^{2}}, ill. 4 t m^{2} + (4 t - 32) m + t = 0 ... \end{matrix}

(2)

egyenletnek a

t

mely értékei mellett van valós megoldása?
Nyilván akkor, ha az egyenlet discriminánsa:

\begin{matrix} {(4 t - 32)}^{2} - 16 t^{2} ≧ 0 vagyis t ≦ 4. \end{matrix}

Eszerint az

O M N △

területének legnagyobb értéke

4

.
A (2) egyenlet gyökeinek összege:

\frac{32 - 4 t}{4 t}

, szorzata:

\frac{t}{4 t} = \frac{1}{4}

.
Ha

0 < t < 4

, a gyökök összege és szorzata is pozitív; így mind a két gyök pozitív.
Ha

t = 4

, akkor

m = \frac{1}{2}

. (Az

M

pontra nézve:

x = 4

y = 2

).
Vizhányó Ferenc (Áll. Szent-István g. VI. o. Bp. XIV.)

Jegyzet. A

t = \frac{32 m}{{(2 m + 1)}^{2}}

függvényt ábrázoló görbe aszimptotikusan közeledik az

X

-tengelyhez.