Kezdőlap


Feladat:	1195. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Baka Sándor , Berényi E. , Blazovich F. , Bleyer L. , Bolgár Imre , Böröcz Imre , Csépes F. , Faludy János , Fellegi Ödön , Freud Géza , Frey E. , Gutmann István , Haraszthy András , Hegedüs Zs. , Hódi Endre , Kaiser K. , Klacskó Géza , Kolozs J. , Kornis Edit , Kovács E. , Kovács L. , Kovács M. , Kulcsár L. , Kunstädter L. , Laub György , Lipsitz Imre , Mandl Tibor , Matolcsy Kálmán , Méry T. , Mészáros György , Mogyoróssy Kálmán , Pallós Károly , Rozsályi Z. , Rubinstein Gy. , Sámuel E. , Steiner Iván , Sulner László , Székely Mária , Szittyai Dezső , Trellay János , Unterberger Gy. , Vendel Z.
Füzet:	1937/november, 73 - 74. oldal		PDF \| MathML
Témakör(ök):	Köréírt alakzatok, Trapézok, Érintőnégyszögek, Négyszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1937/szeptember: 1195. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. A kör $K L$ átmérőjének két végpontjában húzzunk a körhöz érintőket; ezek párhuzamosak, a trapéz párhuzamos oldalainak tartói. A $K$ pontból a trapéz megadott oldalával, mint sugárral kört szerkesztünk, mely az $L$ ponton át húzott érintőt az $M$ (és $M'$ ) pontban metszi. A kör $O$ középpontjából $K M$ -re merőleges sugarat állítunk, ezen sugár $P$ végpontjában a körhöz érintőt húzunk; ezen érintőnek a két párhuzamos érintő közötti darabja $= K M$ és a trapéz $A D$ oldala lesz; $A D$ -vel a $K L$ -re nézve szimmetrikus $B C$ lesz a trapézt bezáró oldal.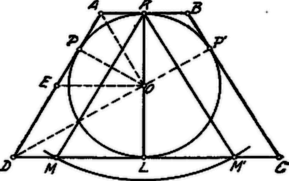

A szerkesztés lehetőségének feltétele, hogy a trapéz megadott oldala

(K M)

a kör átmérőjénél nagyobb legyen.

Haraszthy András (Szent-László g. V. o. Bp. X.)

II. Megoldás. Az érintőnégyszög jellemző tulajdonsága, hogy két-két szembenfekvő oldalának összege egyenlő. Szimmetrikus trapéz esetében a párhuzamos oldalak összege egyenlő a nem párhuzamos oldalak összegével:

a + b = 2 c

, tehát

c = \frac{a + b}{2}

.
A trapéz középvonala eszerint

= c = A D

.
A trapéz középvonala felezi az

A D

-t az

E

pontban.
Ezek alapján a szerkesztést így végezhetjük: a kör

O

középpontján át tetszőleges egyenest húzunk és erre felmérjük az

O E = \frac{c}{2}

távolságot;

E

pontból a körhöz érintőt húzunk és erre felmérjük az

E A = E D = \frac{c}{2}

távolságokat. Az

A

és

D

pontokból a körhöz még egy-egy érintőt húzunk; ezek érintéspontjai

K

L

. A trapéz kiegészítése a

K L

-re való szimmetria alapján történhetik.

Freud Géza (Berzsenyi Dániel g. VI. o. Bp. V.)

Kiegészítés. Igazolnunk kell azonban, hogy

A K ∥ D L

. Ugyanis

O A D Δ

O

-nál derékszögű, mert

O E = E A - E D

. Ezért

O A E ∢ + O D E ∢ = 90^{\circ}

.
Másrészt

O A K ∢ = O A E ∢

és

O D L ∢ = O D E ∢

.
Így

2 (O A E ∢ + O D E ∢) = E A K ∢ + E D L ∢ = 2 \cdot 90^{\circ} = 180^{\circ}

, tehát

A K ∥ D L