Kezdőlap


Feladat:	1193. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Deák András , Freud Géza , Hajdu Á. , Hoffmann Tibor , Matolcsy Kálmán , Steiner Iván
Füzet:	1937/november, 72. oldal		PDF \| MathML
Témakör(ök):	Körülírt kör, Súlypont, Egyenes, Paralelogrammák, Húrnégyszögek, Szélsőérték-feladatok differenciálszámítás nélkül, Gyakorlat
Hivatkozás(ok):	Feladatok: 1937/szeptember: 1193. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{0}$ . Az $A P M Q$ parallelogramma $A M$ és $P Q$ átlói az $O$ középpontban felezik egymást. Eszerint $O$ mindenkor felezi $A M$ -t; $O$ pont távolsága a $B C$ oldaltól mindig a $B C$ oldalhoz tartozó magasság felével egyenlő. Tehát $O$ a $B C$ -vel párhuzamos egyenest ír le, mely az $A B$ és $A C$ oldalakat felezi az $I$ , ill. $J$ pontb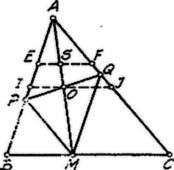an.

A P Q Δ

súlypontja, ‐

S

‐ az

A O

súlyvonalon fekszik úgy, hogy

\begin{matrix} A S = \frac{2}{3} A O = \frac{2}{3} \cdot \frac{A M}{2} = \frac{1}{3} A M \end{matrix}

Tehát

S

is a

B C

-vel párhuzamos egyenest ír le, mely

A B

-t az

E

A C

-t az

F

pontban metszi úgy, hogy

A E = \frac{1}{3} A B

és

A F = \frac{1}{3} A F

2^{0}

. A parallelogramma csak akkor lehet húrnégyszög, ha derékszögű; kell tehát, hogy

B A C ∢ = 90^{\circ}

legyen, azaz a háromszög (

A

-nál) derékszögű.
Ha

A P M Q

így húrnégyszög, akkor

A M

a köréje írt kör átmérője; ez legkisebb akkor, amidőn

A M

B C

átfogóhoz tartozó magasság.

Hoffmann Tibor (Szent-István g. VI. o. Bp. XIV.)