Kezdőlap


Feladat:	1182. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Freud Géza , Grosz László , Halász Iván , Hoffmann Tibor , Juhász Kató , Miklós Erzsébet , Sándor Gyula
Füzet:	1937/október, 40 - 41. oldal		PDF \| MathML
Témakör(ök):	Trapézok, Síkgeometriai számítások trigonometria nélkül körökben, Másodfokú függvények, Mértani középtételek derékszögű háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1937/május: 1182. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{0}$ . Ha $M$ vetülete 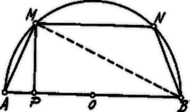$A B$ -n $P$ , akkor

\begin{matrix} {\bar{A M}}^{2} = \bar{A B} \cdot \bar{A P} = 2 R (A O - P O) = 2 R (R - \frac{x}{2}) \\ {\bar{A M}}^{2} = {\bar{N B}}^{2} = 2 R^{2} - R x \\ és így y = {\bar{A M}}^{2} + {\bar{M N}}^{2} + {\bar{N B}}^{2} = 2 (R^{2} - R x) + x^{2} \\ y = x^{2} - 2 R x + 4 r^{2} = {(x - R)}^{2} + 3 R^{2} . \end{matrix}

x

értéke változhatik

0

-tól

2 R

-ig.
Ha

x = 0

, a trapézból egyenlőszárú derékszögű háromszög lesz és

y = 4 R^{2}

.
Ha

x = 2 R

, a trapéz az

A B

vonaldarabbá zsugorodik össze; ekkor

y = 4 R^{2}

.
Láthatjuk, hogy

y

-nak minimuma:

3 R^{2}

áll elő, ha

x = R

. Ezen esetben

A M = M N = N B = R

; a szimmetrikus trapéz a körbe írt szabályos hatszög fele.

Eszerint

y

értéke

4 R^{2}

-től csökken

3 R^{2}

-ig, azután növekszik

4 R^{2}

-ig. A változást egy parabola íve tünteti fel, mely keresztül megy a csúcson és szimmetrikus a főtengelyére nézve.

\begin{matrix} [Ha pl . R = 1, y = {(x - 1)}^{2} + 3 = x^{2} - 2 x + 4] . \end{matrix}

2^{0}

. Ha

y = a^{2}

, akkor az

{(x - R)}^{2} + 3 R^{2} = a^{2}

egyenletet kell megoldanunk, tehát

\begin{matrix} x = R \pm \sqrt[]{a^{2} - 3 R^{2}} . \end{matrix}

Valós megoldás akkor van, ha

a^{2} ≧ 3 R^{2}

.
Ha

a^{2} < 4 R^{2}

, akkor az

\begin{matrix} x^{2} - 2 R x + 4 R^{2} - a^{2} = 0 \end{matrix}

egyenlet mindkét gyöke pozitív és

2 R

-nél kisebb, mert szorzatuk:

4 R^{2} - a^{2} > 0

és összegük

2 R > 0

.
Ha

a^{2} > 4 R^{2}

, akkor a gyökök szorzata negatív: az egyik gyök pozitív a másik negatív; a pozitív gyök

> 2 R

és így egyik gyök sem felel meg.
A függvénygörbe segítségével a megoldás: a megadott

y

értéknek megfelelőleg az

X

-tengellyel párhuzamosat húzunk. Ezen párhuzamosnak a görbével való közös pontjai (ill. ezek abscissái) szolgáltatják az egyenlet gyökeit. Ilyen közös pontok csak akkor léteznek, ha

\begin{matrix} 3 R^{2} \leq y = a^{2} \leq 4 R^{2} . \end{matrix}

y = a^{2} = 3 R^{2}

esetben érintkezés áll elő és így csak egy megoldás van.

y

többi értékeinél két megoldás van.