Kezdőlap


Feladat:	1173. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bulkay Lajos , Deák András , Freud Géza , Halász Iván , Hoffmann Tibor , Kemény Miklós , Klein József , Margulit György , Matolcsy Kálmán , Rotter Éva , Sándor Gyula , Steiner Iván , Száva I. , Tornai Jenő , Vásárhelyi Nagy Sándor , Vecsés J.
Füzet:	1937/szeptember, 7 - 8. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül, Terület, felszín, Trapézok, Húrnégyszögek, Síkgeometriai bizonyítások, Gyakorlat
Hivatkozás(ok):	Feladatok: 1937/április: 1173. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{0}$ . A négyszög negyedik oldala, $D A$ oly húr, amely

\begin{matrix} 360^{\circ} - (60^{\circ} + 90^{\circ} + 120^{\circ}) = 90^{\circ} -ú \end{matrix}

ívhez tartozik. A négyszög szimmetrikus trapéz, mert

B C = D A

és

A B ∥ C D

.
Már most

A B

a szabályos hatszög oldala

= R

B C = A D

a körbe írt négyzet oldala

= R \sqrt[]{2}

C D

a körbe írt szabályos háromszög oldala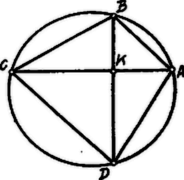

= R \sqrt[]{3}

2^{0}

. Az átlók által bezárt szög mértéke, az általuk kimetszett ívek összegének a fele:

\begin{matrix} \frac{1}{2} (\hat{A B} + \hat{C D}) = \frac{1}{2} \cdot 180^{\circ} = 90^{\circ} = \frac{1}{2} (\hat{B C} + \hat{C D}) . \end{matrix}

A szimmetrikus trapéz átlói egyenlők:

A C = B D

. Metszéspontjuk legyen

K

. A

C K D Δ

egyenlőszárú, mert

C D K ∢ \equiv C D B ∢ = \frac{1}{2} \hat{B C} = 45^{\circ}

.
Ezért

\begin{matrix} D K = C K = \frac{C D}{\sqrt[]{2}} = R \sqrt[]{\frac{3}{2}} . \end{matrix}

A K D Δ

olyan derékszögű háromszög, amelyben az

\begin{matrix} A D K ∢ = \frac{1}{2} \hat{A B} = 30^{\circ} és így K A = \frac{1}{2} A D = \frac{1}{2} R \sqrt[]{2} . \end{matrix}

Hasonlóan látható, hogy

B K = K A

3^{0}

A négyszög területe

\begin{matrix} \frac{1}{2} C A \cdot B K + \frac{1}{2} C A \cdot D K = \frac{1}{2} C A (B K + K D) = \frac{1}{2} C A \cdot B D = \frac{1}{2} {\bar{C A}}^{2} . \\ = \frac{1}{2} {(R \sqrt[]{\frac{3}{2}} + \frac{1}{2} R \sqrt[]{2})}^{2} = \frac{R^{2}}{4} {(\sqrt[]{3} + 1)}^{2} = R^{2} \frac{2 + \sqrt[]{3}}{2} . \end{matrix}

Deák András (Érseki g. V. o. Bp. II.).

Jegyzet.

\bar{C A} \cdot \bar{B D} = {\bar{C A}}^{2}

a Ptolemaeus-tétel alapján is számítható.