Kezdőlap


Feladat:	1163. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Fehérváry Ákos , Grosz László , Jakab Károly , Steiner Iván
Füzet:	1937/május, 272 - 273. oldal		PDF \| MathML
Témakör(ök):	Mértani helyek, Síkgeometriai bizonyítások, Körülírt kör középpontja, Egyenes, Gyakorlat, Súlyvonal
Hivatkozás(ok):	Feladatok: 1937/március: 1163. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ismeretes, hogy a derékszögű háromszög átfogójának felezőpontja $O$ , a derékszögű háromszög köré írt kör középpontja, tehát $O A = O B = O C$ és így ${\bar{O B}}^{2} + {\bar{O C}}^{2} = 2 O A^{2}$ . Ez annyit jelent, hogy az $O$ pont a szóbanforgó mértani hely egyik pontja.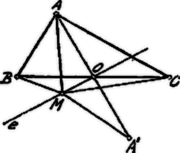

Legyen már most

M

a sík valamely pontja:

M O

M B C Δ

egyik súlyvonala; ezért

\begin{matrix} {\bar{M B}}^{2} + {\bar{M C}}^{2} = 2 {\bar{M O}}^{2} + 2 {\bar{O B}}^{2} ... \end{matrix}

(1)

Ha pedig

A'

A

szimmetrikus pontja

O

-ra nézve, akkor

M O

M A A' Δ

súlyvonala és így

\begin{matrix} {\bar{M A}}^{2} + \bar{M A}'^{2} = 2 {\bar{M O}}^{2} + 2 {\bar{O A}}^{2} = 2 {\bar{M O}}^{2} + 2 {\bar{O B}}^{2} ... \end{matrix}

(2)

1)-ből és 2)-ből

\begin{matrix} {\bar{M B}}^{2} + {\bar{M C}}^{2} = {\bar{M A}}^{2} + \bar{M A}'^{2} ... \end{matrix}

(3)

a sík bármely

M

pontjára nézve. Ha azonban

M

eleget tesz az

\begin{matrix} {\bar{M B}}^{2} + {\bar{M C}}^{2} = 2 {\bar{M A}}^{2} \end{matrix}

feltételnek, akkor nyilván

{\bar{M A}}^{2} = \bar{M A}'^{2}

, ill.

\bar{M A} = M A'

, azaz az

M

pont azon egyenes pontja, mely

\bar{A A}'

-t az

O

pontban merőlegesen felezi.
Megfordítva: a 3) összefüggés a sík minden pontjára érvényes; ha pedig

M A' = M A

, akkor

2 {\bar{M A}}^{2} = {\bar{M B}}^{2} + {\bar{M C}}^{2}

, tehát az

A A'

-t merőlegesen felező egyenes valóban mértani helye azon

M

pontoknak, amelyekre nézve

\begin{matrix} {\bar{M B}}^{2} + {\bar{M C}}^{2} = 2 {\bar{M A}}^{2} . \end{matrix}

Jegyzet. A beérkezett megoldások jelentékeny része csak azt bizonyítja, hogy az átfogó

O

felező pontja eleget tesz a feltételnek. Hogy a mértani hely egyenes, azt a feladat szövege alapján fogadják el.