Feladat: 1149. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Amigo György ,  Bagdy Dániel ,  Bleyer Jenő ,  Bleyer L. ,  Danciger E. ,  Dudás Imre ,  Fekete András ,  Freud Géza ,  Grosz László ,  Grünfeld Sándor ,  Havas I. ,  Jakab Károly ,  Joó Endre ,  Klein József ,  Kovács Mátyás ,  Lipsitz Imre ,  Matolcsy Kálmán ,  Névtelen ,  Sándor Gyula ,  Sommer György ,  Steiner Iván ,  Tóth B. ,  Vásárhelyi Nagy Sándor 
Füzet: 1937/április, 234 - 235. oldal  PDF  |  MathML 
Témakör(ök): Egyenlőtlenségek grafikus megoldása, Másodfokú (és arra visszavezethető) egyenlőtlenségek, Hiperbola, mint kúpszelet, Gyakorlat
Hivatkozás(ok):Feladatok: 1937/február: 1149. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. a) Ha x(x+1)x-1>3, akkor

x(x+1)x-1-3>0,ill.x(x-1)-3(x-1)x-1=x2-2x+3x-1>0.

Azonban x2-2x+3=(x-1)2+2>0 az x bármely értékénél és így akkor van kielégítve az egyenlőtlenség, ha
x-1>0,azazx>1.

b) Ebben az esetben x(x+1)x-1-6=x(x+1)-6(x-1)x-1=x2-5x+6x-1>0.
Minthogy x2-5x+6=(x-2)(x-3), kell, hogy legyen:
(x-2)(x-3)x-1>0vagy(x-2)(x-3)(x-1)>0.
Ez bekövetkezik akkor, ha a baloldali tényezők mindegyike pozitív, azaz ha x>3, vagy pedig, ha egyik tényező pozitív, a másik kettő negatív. Utóbbi eset akkor áll elő, ha 1<x<2.*
Sándor Gyula (Kölcsey Ferenc rg. VI. o. Bp. VI.)

 

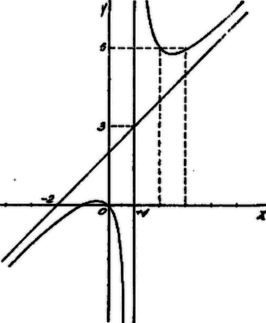
II. Megoldás. Ábrázoljuk az
y=x2+xx-1=x(x+1)x-1
függvényt. Ennek oly hiperbola felel meg, melynek egyik aszimptotája az x=1 egyenes.
Ha x=-∞, akkor y=-∞. Mindaddig, amíg x<-1, y<0, x=-1 és x=0 helyeken y=0. A -1<x<0 közben y>0.
A 0<x<1 közben y<0 és ha x közeledik ezen közben az 1-hez, y a -∞ felé tart.
Ha x>1, akkor y>0, még pedig +∞-től csökken egy bizonyos értékig, azután a +∞ felé tart.
A függvény ábrázolására szolgáljon a következő értéktáblázat:
|x-∞...-3-2-1-0,4200,5+1y-∞↗-1,5-2300,17max0-2,5-∞

|+122,4134...+∞+∞↘65,83min6203↗+∞

 
 

A grafikonból látjuk, hogy, ha x>1, y>3, mert hiszen y legkisebb értéke 3+22.
y>6,ha1<x<2és hax>3.

Amigo György (Izr. rg. VI. o. Debrecen).
 

Kiegészítés. x minden értékéhez ‐ az x=1 helyet kivéve ‐ tartozik egy ‐ és csakis egy y érték. Megfordítva: nem minden y értékhez tartozik x érték.
Rendezzük a függvény-kapcsolatot x szerint. A tört eltávolítása után keletkezik:
x2+(1-y)x+y=0.

Adott y értékhez akkor kapunk x értéket, ha ezen egyenlet discriminánsa
D≡(1-y)2-4y≥0,ill.D≡y2-6y+1≥0.

Ha D=0, akkor x1=x2=y-12.
Ha D>0, akkor az egyenletnek két különböző valós gyöke van.
D=0, ha y=3±22. Ezen értékek mindegyikéhez egy x érték tartozik. Még pedig y=3-22∼0,17, a függvény maximuma*; ez akkor áll elő, ha x∼-0,42.
y=3+22∼5,83, a függvénynek minimuma és ekkor x∼2,41.*
Ha már most 3-22<y<3+22, akkor x nem valós. Más szóval: ha az X-tengellyel párhuzamosan, tőle 3-22, ill. 3+22 távolságban egyeneseket húzunk, ezek a görbe egy-egy ágát érintik a felső, ill. alsó tetőpontjukban. E két egyenes közötti síkrészen a görbének nincs pontja. A görbe pontjai csak az y≤3-22 ill. y≧3+22 értékekhez tartoznak.
Az (x=1, y=3) pont a görbe középpontja. Ezen ponton keresztül húzható a hiperbola másik aszimptotája, mely az X-tengelyhez 45∘-ú szög alatt hajlik.
*Ha x<1, mindegyik tényező negatív.
Ha 2<x<3, akkor x-3<0, a másik két tényező pozitív.

*Felső tetőpont a görbe azon ágán, mely az x=1 egyenestől balra fekszik.

*Alsó tetőpont a görbe másik ágán.