Kezdőlap


Feladat:	1143. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Baranyai György , Bleyer Jenő , Bleyer L. , Grünfeld Sándor , Jakab Károly , Katz M. , Lipsitz Imre , Sándor Gyula
Füzet:	1937/március, 202. oldal		PDF \| MathML
Témakör(ök):	Paralelogrammák, Síkgeometriai számítások trigonometria nélkül háromszögekben, Háromszögek szerkesztése, Gyakorlat, Súlyvonal, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 1937/január: 1143. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A háromszög súlyvonalai, $A A_{1}$ , $B B_{1}$ , $C C_{1}$ , ahol $A_{1}$ , $B_{1}$ , $C_{1}$ rendre a $B C$ , $C A$ , $A B$ oldalak felezőpontjai. Tudjuk, hogy a súlyvonalak a háromszög $S$ súlypontján mennek keresztül úgy, hogy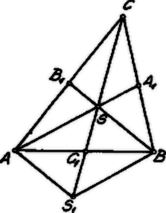

\begin{matrix} A S : S A_{1} = B S : S B_{1} = C S : S C_{1} = 2 : 1. \end{matrix}

Hosszabbítsuk meg pl. az

S C_{1}

-et a

C_{1} S_{1} = S C_{1} = \frac{1}{3} C C_{1}

távolsággal. Ekkor

A S B S_{1}

idom parallelogramma, mert átlói:

S S_{1}

és

A B

C_{1}

pontban felezik egymást.
Ebből következik:

A S_{1} = B S = \frac{2}{3} B B_{1}

.
Azonban

A S = \frac{2}{3} A A_{1}

és

S S_{1} = \frac{2}{3} C C_{1}

, tehát az

A S S_{1} Δ

oldalai:

\frac{2}{3} A A_{1}, \frac{2}{3} B B_{1}, \frac{2}{3} C C_{1}

.
Ha a súlyvonalak

\frac{2}{3}

részeivel tudtunk háromszöget szerkeszteni, akkor az egész súlyvonalakkal is tudunk. (A súlyvonalakkal szerkesztett háromszög hasonló az

A S S' Δ

-höz).

Baranyai György (Áll. Dobó István r. IV. o. Eger).

Jegyzet. A többi megoldások szerzői félreértették a feladatot. T. i. azt gondolták, hogy ha adva vannak a háromszög súlyvonalai, szerkesszük meg a háromszöget. Holott itt arról volt szó, hogy a súlyvonalak maguk lehetnek egy háromszög oldalai. (Bármely két súlyvonal összege nagyobb a harmadiknál.)