Kezdőlap


Feladat:	1142. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Fehérváry Ákos , Joó Endre , Steiner Iván , Szűcs F. , Tornai Jenő
Füzet:	1937/március, 201 - 202. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Függvényvizsgálat, Terület, felszín, Trapézok, Deltoidok, Szélsőérték-feladatok differenciálszámítás nélkül, Gyakorlat
Hivatkozás(ok):	Feladatok: 1937/január: 1142. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $E F ∥ H G ∥ B D$ és $O A = m_{1}$ , $O C = m_{2}$ . Az $E F G H$ idom szimmetrikus trapéz (az $A C$ tengelyre nézve). Ha a rövidség kedvéért $E F = u, H G = v$ , akkor tekintettel arra, hogy a trapéz magassága $2 x$ , a trapéz területe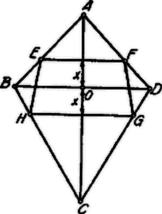

\begin{matrix} y = \frac{u + v}{2} \cdot 2 x = u x + v x . \end{matrix}

\begin{matrix} A B D Δ \sim A E F Δ; ezért B D : E F = O A : I_{1} A, \end{matrix}

vagyis

\begin{matrix} d : u = m_{1} : (m_{1} - x), tehát u = d - \frac{d}{m_{1}} x . \\ B C D Δ \sim H G C Δ; ezért B D : H G = O C : I_{2} A, \end{matrix}

vagyis

\begin{matrix} d : v = m_{2} : (m_{2} - x), \end{matrix}

és így

\begin{matrix} v = d - \frac{d}{m_{2}} x . \end{matrix}

Ezek alapján

\begin{matrix} y = 2 d x - \frac{d (m_{1} + m_{2})}{m_{1} m_{2}} x^{2} . \end{matrix}

Vizsgálnunk kell e függvényt, ha

0 \leq x \leq m_{1}

. (Ugyanis

m_{1} < m_{2}

). Ha

x = 0, y = 0

; ekkor a trapéz a

B D

vonaldarabbá zsugorodik össze. Ha

x = m_{1}

, akkor

\begin{matrix} y = 2 d m_{1} - \frac{d (m_{1} + m_{2})}{m_{1} m_{2}} m_{1}^{2} = \\ = \frac{1}{m_{2}} (2 d m_{1} m_{2} - d m_{1}^{2} - d m_{1} m_{2}) = \frac{d m_{1} (m_{2} - m_{1})}{m_{2}} . \end{matrix}

Ebben az esetben a trapéz

A G H Δ

-be megy át, melynek alapja:

\frac{d (m_{2} - m_{1})}{m_{2}}

és magassága

2 x = 2 m_{1}

.
A függvénynek maximuma van, ha

\begin{matrix} x = \frac{m_{1} m_{2}}{m_{1} + m_{2}} < m_{1} és ekkor y_{max} = \frac{m_{1} m_{2}}{m_{1} + m_{2}} d . \end{matrix}

Az adott numerikus értékekkel:

\begin{matrix} m_{1}^{2} = {\bar{O A}}^{2} = {\bar{A B}}^{2} - {\bar{O B}}^{2} = 5^{2} - 3^{2} = 4^{2}; m_{1} = 4, \\ m_{2}^{2} = {\bar{O C}}^{2} = {\bar{B C}}^{2} - {\bar{O B}}^{2} = 45 - 9 = 6^{2}; m_{2} = 6. \end{matrix}

Így

\begin{matrix} y = - 2, 5 x^{2} + 12. \end{matrix}

E függvény ábrázolására szolgáló néhány érték: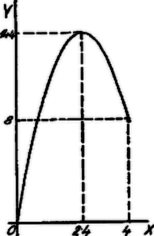

\begin{matrix} \begin{matrix} x & 0 & 1 & 2 & 2, 4 & 2, 8 & 3 & 3, 5 & 4 \\ y & 0 & 9, 5 & 14 & 14, 4 & 14 & 13, 5 & 11, 1 & 8 \\ max \end{matrix} \end{matrix}