Feladat: 1124. matematika gyakorlat Korcsoport: 14-15 Nehézségi fok: -
Megoldó(k):  Amigó György ,  Bagdy Dániel ,  Baranyai Gy. ,  Berényi E. ,  Bleyer Jenő ,  Bleyer M. ,  Czeiczler Gy. ,  Deák András ,  Dudás Imre ,  Fehérváry Ákos ,  Fekete András ,  Fodor P. ,  Füleky Lajos ,  Guttmann A. ,  Hahn István ,  Hajnal Miklós ,  Halász Iván ,  Havas I. ,  Holnapy K. ,  Joó Endre ,  Klein József ,  Kovalóczy Gy. ,  Lichtenberg Erzsébet ,  Lipsitz Imre ,  Marton L. ,  Monath Ferenc ,  Nádasdy J. ,  Papp Attila ,  Rotter Éva ,  Rubinstein Gy. ,  Steiner Iván ,  Székely Mária ,  Székely Z. ,  Szilárd Rezső ,  Szittyai Dezső ,  Tóth D. ,  Tóth I. ,  Vass L. ,  Vecsés J. ,  Vértessy Lajos ,  Wiczay Imre 
Füzet: 1937/január, 145 - 146. oldal  PDF  |  MathML 
Témakör(ök): Derékszögű háromszögek geometriája, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):Feladatok: 1936/november: 1124. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Az A ponton keresztül e1-, ill. e2-re húzott merőleges e1-t a H, e2-t a K pontban metszi. HK=d a két párhuzamos egyenes egymástól való távolsága. Feltesszük, hogy 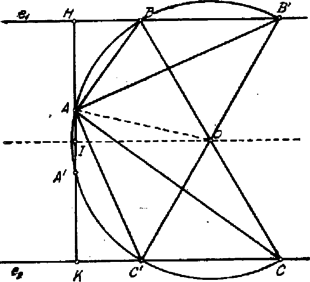a≥d.
Ha BACΔ a követelménynek megfelel, akkor a BC mint átmérő felett szerkesztett kör keresztülmegy az A ponton. Minthogy e kör középpontja, O, a BC felező pontja, a HK-t az A ponton kívül még egy A pontban metszi, amely A-val szimmetrikus HK felezőpontjára, I-re nézve.
 
 

Az O pont eszerint megszerkeszthető; ugyanis O metszéspontja az A középpontból a2 sugárral szerkesztett körnek és az Ix egyenesnek, amely párhuzamos e1-, ill. e2-vel. Ha ilyen módon O-t megkapjuk, akkor O-ból a2(>d2) sugárral kört szerkesztünk, mely az e1-t a B és B', az e2-t a C' és C pontokban metszi úgy, hogy B és C, ill. B' és C' diametrálisan szemben fekvő pontok. Ilyenformán két megoldásunk van: BAC és B'A'C'.
Ha O nak az I-re nézve szimmetrikus pontját vesszük és ugyanúgy járunk el, mint az előbb, akkor az előbbi két háromszöggel, HK-ra szimmetrikus helyzetű megoldásokat kapunk.
 

Bagdy Dániel (Fazekas Mihály r. VI. o. Debrecen).



II. Megoldás. Jelöljünk ki az e1 egyenesen valamely tetszőleges B0 pontot. Innen, mint középponttól a(>d) sugárral körívet szerkesztünk, mely e2-t két pontban metszi; ezek egyike legyen C0. Már most B0C0 mint átmérő felett kört szerkesztünk; A-ból az e1, ill. e2-vel párhuzamost húzva, ez A1 és A2-ben metszi e kört. B0A1C0 és B0A2C0 derékszögű háromszögek, amelyeket most A1A-, ill. A2A-val el kell tolnunk úgy, hogy oldalaik önmagukkal párhuzamosak maradnak: így B1AC1 és B2AC2 lesznek a megfelelő háromszögek.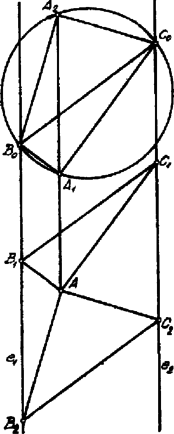
 
 

Két megoldást kapunk még (az előbbiekkel szimmetrikus helyzetűeket), ha a B0 pontból a sugárral szerkesztett körívnek az e2-vel való másik metszéspontjából indulunk ki.
 

Hajnal Miklós (izr. rg. VI. o. Bp.).