Kezdőlap


Feladat:	1092. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bagdy D. , br. Splény G. , Dudás I. , Fekete A. , Halász I. , Holzer Pál , Kondor I. , Mandl B. , Nagy E. , Németh K. , Radovics Gy. , Seidl G. , Somogyi A.
Füzet:	1936/október, 39. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Párhuzamos szelők tétele, Háromszögek szerkesztése, Síkgeometriai szerkesztések, Gyakorlat
Hivatkozás(ok):	Feladatok: 1936/május: 1092. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Az aránypárokra vonatkozó átalakítási szabályok alkalmazásával írhatjuk, hogy ha

\begin{matrix} \frac{p}{a - c} = \frac{a + c}{a}, akkor \frac{2 (a - c) - p}{a - c} = \frac{2 a - (a + c)}{a}, \end{matrix}

azaz

\begin{matrix} \frac{2 (a - c) - P}{a - c} = \frac{a - c}{a} . \end{matrix}

Az így keletkező aránypárnak 3 tagja adva lévén, a negyedik, t. i.

a

, megszerkeszthető, hacsak

\begin{matrix} 2 (a - c) > p, azaz a - c > \frac{p}{2} . \end{matrix}

O

pontból kiinduló

e_{1}

sugáron legyen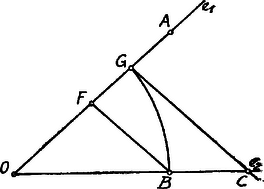

O A = p

és az

e_{2}

-n

O B = a - c

O F = 2 O B - O A

és

O G = O B

, a

G

-ből

F B

-vel párhuzamosan vont szelő a

C

pontban metszi

e_{2}

-t, úgy, hogy

\begin{matrix} O C = a és B C = c, \end{matrix}

mert

\begin{matrix} O F : O B = O G : O C . \end{matrix}

II. Megoldás. Legyen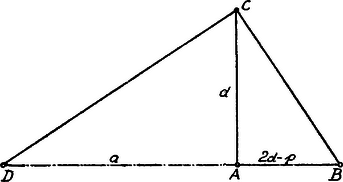

a - c = d

, tehát

c = a - d

. Ekkor

\begin{matrix} \frac{p}{d} = \frac{2 a - d}{a} és innen d^{2} = a (2 d - p) . \end{matrix}

Eszerint

d

mértani középarányosa

a

-nak és

(2 d - p)

-nek. Oly derékszögű háromszöget kell szerkesztenünk, amelyben az átfogóhoz tartozó magasság

d

és az átfogó egyik szelete

2 d - p

. Az átfogó másik szelete lesz

a

Ha tehát

A B = 2 d - p

és a reá merőleges

A C = d

, akkor a

C

pontban

B C

-re merőlegest állítunk. Ezen merőleges

A B

tartóját a

D

pontban metszi úgy, hogy

A D = a

Holzer Pál (Faludi Ferenc rg. VI. o. Szombathely.)