Feladat: 1091. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bagdy Dániel ,  Bluszt E. ,  Donáth G. ,  Dudás I. ,  Fekete A. ,  Halász I. ,  Holzer P. ,  Kalamaznik N. ,  Kemény Gy. ,  Kondor I. ,  Mandl B. ,  Marosán Z. ,  Nagy E. ,  Németh K. ,  Radovics Gy. ,  Schreiber B. ,  Seidl G. ,  Somogyi A. ,  Splény G. 
Füzet: 1936/október, 38 - 39. oldal  PDF  |  MathML 
Témakör(ök): Derékszögű háromszögek geometriája, Terület, felszín, Paralelogrammák, Szélsőérték-feladatok differenciálszámítás nélkül, Gyakorlat
Hivatkozás(ok):Feladatok: 1936/május: 1091. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Minthogy E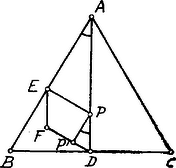AP∢=30∘ és PE⊥AB, PE=AP2=h-x2.
Bocsássunk P-ből DF-re is merőlegest, PP'-t; ekkor P'PD∢=30∘ és PP'=PD32=x32.

 
 

Így a paralelogramma területe

y=DF⋅PP'=PE⋅PP'=h-x2⋅x32=34x(h-x),(1)y=-34(x2-hx)=-34[(x-h2)2-h24]y=h2316-(x-h2)2.(2)



A függvény (1) alatti alakjából látjuk, hogy a paralelogramma területe eltűnik, ha x=0 és ha x=h, azaz ha a P pont D-ben ill. A-ban van.
A (2) alatti alakjából pedig kiolvassuk, hogy y értéke legnagyobb, ha x=h2 és ekkor ymax=h2316.
Eszerint a paralelogramma területe zérusról növekedik h2316-ig, ezen értékét akkor veszi fel, amidőn a P pont telezi AD-t. Innen azután csökken zérusig.
A terület változását egy parabolának az X-tengely felett fekvő íve tünteti fel; a parabola tengelye az x=h2 egyenes. A parabola keresztül megy az x=p, y=0 és x=h, y=0 pontokon; x=h2, y=h2316 a parabola felső tetőpontját határozza meg.
 

Bagdy Dániel (Fazekas Mihály r. V. o. Debrecen.)
 

Jegyzet. Hivatkozhattunk volna arra is, hogy ha két szám összege állandó, szorzatuk legnagyobb akkor, amidőn a két szám egyenlő egymással (mégpedig az állandó összegük felével). Az (1) alatt szereplő
x(h-x)
szorzat tényezőinek összege: x+h-x=h. A szorzat értéke legnagyobb, ha
x=h-x,ill.x=h2.