Kezdőlap


Feladat:	1085. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Bluszt E. , Donáth S. , Dudás I. , Elek Gy. , Fehérváry Á. , Fekete András , Füleky Lajos , Földi M. , Halász I. , Kalamaznik J. , Kemenes F. , Kemény Gy. , Komlós J. , Korényi I. , Kormoss I. , Mandl B. , Marosán Z. , Méri B. , Nagy E. , Papp I. , Radovics Gy. , Róth P. , Sebestyén Gyula , Seidl G. , Somogyi A. , Tóth B.
Füzet:	1936/szeptember, 14 - 15. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Derékszögű háromszögek geometriája, Négyzetek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1936/április: 1085. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Jelentsék $a$ és $b$ egy derékszögű háromszög befogóit, $c$ az átfogót; így $c^{2} = a^{2} + b^{2}$ . Eszerint $a^{2} + b^{2}$ jelenti az átfogó fölé szerkesztett négyzet területét.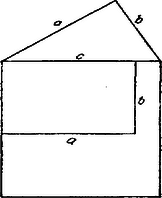
$a b$ jelenti oly téglalap területét, amelynek oldalai $a$ és $b$ .

Minthogy

a < c

és

b < c

, ezen téglalap benne van ‐ ábránk szerint feltüntetve ‐ a

c

oldalú négyzetben. Tehát a

c

oldalú négyzet területe nagyobb a téglalapénál és így valóban áll:

\begin{matrix} a^{2} + b^{2} > a b . \end{matrix}

Sebestyén Gyula (Fazekas Mihály r. VI. o. Debrecen.)

Jegyzet. Nyilván, ha

a ≧ b

, akkor

a^{2} ≧ a b

, tehát

\begin{matrix} a^{2} + b^{2} > a b . \end{matrix}

II. Megoldás.

c^{2} = a^{2} + b^{2}

jelenti, ha

a

és

b

egy derékszögű háromszög befogói, oly négyzet területét, melynek oldala a derékszögű háromszög átfogója.
Rajzoljuk meg tehát a derékszögű háromszöget,

a

és

b

befogókkal és szerkesszük meg a körülírt körét, melynek átmérője

c

. Ezen kört érintő négyzet területe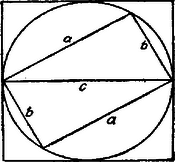

c^{2} = a^{2} + b^{2}

a b

jelenti oly téglalap területét, mely

a

és

b

oldalakkal az előbbi körbe írt négyszög.
Ilyen négyszög területe mindig kisebb az érintő négyszög területénél. (Bármely húrsokszög területe kisebb valamely ‐ ugyanazon kör köré írt ‐ érintő sokszög területénél.)

Füleky Lajos (Koháry István rg. V. o. Gyöngyös.)

III. Megoldás. Ha

a

és

b

ismét a derékszögű háromszög befogói és

c

az átfogója, akkor az átfogó fölé szerkesztett négyzet, ábránk szerint, öt részre osztható.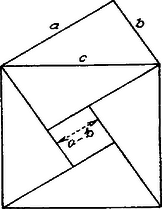

Ezek közül négy az eredeti derékszögű háromszöggel egybevágó, az ötödik rész egy négyzet, melynek oldala

a - b

. Tehát a négyzet területe

\begin{matrix} c^{2} = 4 \cdot \frac{a b}{2} + {(a - b)}^{2}, azaz a^{2} + b^{2} = 2 a b + {(a - b)}^{2} \end{matrix}

és így valóban:

\begin{matrix} a^{2} + b^{2} > a b . \end{matrix}

Fekete András (Fazekas Mihály r. V. Debrecen.)