Kezdőlap


Feladat:	1081. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bagdy D. , Donáth G. , Dudás I. , Fehérváry Á. , Fekete A. , Halász I. , Holzer P. , Jakab Károly , Komlós J. , Kondor I. , Mandl Béla , Nagy E. , Németh K. , Papp I. , Radovics Gy. , Sebestyén Gy. , Somogyi A. , Somogyi I. , Tóth B.
Füzet:	1936/szeptember, 11 - 12. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Derékszögű háromszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1936/április: 1081. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A $B C$ húr felezőpontja legyen $D$ , továbbá a kör sugara 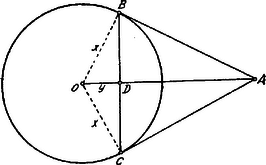$O B = O C = x$ és $O D = y$ .

O A B

derékszögű háromszögben

\begin{matrix} {\bar{O B}}^{2} = \bar{O A} \cdot \bar{O D}, azaz x^{2} = a y \end{matrix}

(1)

és

\begin{matrix} {\bar{B D}}^{2} = \bar{O D} \cdot \bar{D A}, azaz ℓ^{2} = y (a - y) . \end{matrix}

(2)

(1)-ből

y = \frac{x^{2}}{a}

. Helyettesítve ezt (2) be, a törtek eltávolítása után az

\begin{matrix} x^{4} - a^{2} x^{2} + a^{2} ℓ^{2} = 0 \end{matrix}

(3)

egyenlethez jutunk, mely

x^{2}

-re nézve másodfokú. Ezen egyenlet gyökei megfelelnek, ha valósak, pozitívek,

a^{2}

-nél kisebbek, de

ℓ^{2}

-nél nagyobbak.
A (3) gyökei valósak, ha

a^{4} - 4 a^{2} ℓ^{2} \geq 0

, ill. ha

a^{2} ≧ 4 ℓ^{2}

, tehát, ha

\begin{matrix} 2 ℓ ≦ a . \end{matrix}

Ha valósak, nyilván pozitívek, mert összegük (t. i.

a^{2}

) és szorzatuk (t. i.

a^{2} ℓ^{2}

) pozitív.
Minthogy (3) alapján

x^{2} (a^{2} - x^{2}) = a^{2} ℓ^{2} > 0

, a gyökök mindegyike

a^{2}

nél kisebb.
Azt kell még megvizsgálnunk, hogy a gyökök nagyobbak-e

ℓ^{2}

-nél? Meg kell néznünk tehát

x^{2} = z

helyettesítésével az

\begin{matrix} f (z) = z^{2} - a^{2} z + a^{2} ℓ^{2} \end{matrix}

függvény előjelét a

z = 0

és

z = ℓ^{2}

helyeken.

\begin{matrix} f (O) = a^{2} ℓ^{2} > 0 és f (ℓ^{2}) = ℓ^{4} - a^{2} ℓ^{2} + a^{2} ℓ^{2} = ℓ^{4} > 0, \end{matrix}

azaz: vagy mind a két gyök 0 és

ℓ^{2}

között, vagy mind a kettő a 0 és

ℓ^{2}

közén kívül van.

Minthogy az

f (z) = 0

egyenlet gyökeinek félösszege

\frac{a^{2}}{2} > ℓ^{2}

, (mert

a^{2} ≧ 4 l^{2}

), a gyökök mindegyike nagyobb

ℓ^{2}

-nél.
Eszerint a feladat megoldható, ha a

B C

húr hossza nem nagyobb az

O A

távolságnál. Két megoldás van, ha

2 ℓ > a

, egy megoldás ha

2 ℓ = a

.
A (3) gyökei

\begin{matrix} x = \frac{a}{2} \sqrt[]{2 \pm 2 \sqrt[]{1 - \frac{4 ℓ^{2}}{a^{2}}}} . \end{matrix}

alakban írhatók.

Mandl Béla (Zrínyi Miklós rg. VI. o. Bp. VIII.)

Geometriai megoldás. A

B

pont két mértani helyen fekszik. Az egyik mértani hely az

O A

átmérő felett szerkesztett kör (u. i.

O B A ∢ = 90^{\circ}

. A másik mértani hely az

O A

-val párhuzamos egyenes, melynek távolsága

O A

-tól

= ℓ

. Ezen egyenes az előbbi kört két pontban metszi, ha

ℓ < \frac{a}{2}

, érinti, ha

ℓ = \frac{a}{2}

. Nincs közös pontjuk, ha

ℓ > \frac{a}{2}

Jakab Károly (Jézustársasági g. VI. o. Kalocsa.)