Feladat:	1035. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Amigó Gy. ,  Bluszt E. ,  br. Karg Irma ,  Brill J. ,  Cseh S. ,  Cserhalmi A. ,  Donáth G. ,  Egger G. ,  Einhorn Ilona ,  Fehérváry Á. ,  Gábor Gy. ,  Guttman A. ,  Holzer P. ,  ifj. Jankovich I. ,  Kalamaznik N. ,  Kemény Gy. ,  Komlós J. ,  Kondor I. ,  Major L. ,  Mandl B. ,  Manninger Olga ,  Marosán Z. ,  Mészáros I. ,  Nagy Elemér ,  Németh K. ,  Pichler László ,  Radovics Gy. ,  Rotter Éva ,  Schreiber B. ,  Szabó A. ,  Szabó L. ,  Szenes Anna ,  Tamás Gy. ,  Tassonyi K. ,  Tóbiás I. ,  Tóbiás K.
Füzet:	1936/január, 142 - 143. oldal		PDF  |  MathML
Témakör(ök):	Háromszögek egybevágósága, Kör (és részhalmaza), mint mértani hely, Síkgeometriai szerkesztések, Ellipszis, mint kúpszelet, Parabola, mint mértani hely, Gyakorlat
Hivatkozás(ok):	Feladatok: 1935/november: 1035. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.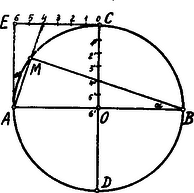     a) Ábránk szerint legyen $n=6$ és $k=4$. Kössük össze tehát $A$-t a $CE$-n jelzett 4, míg $B$-t a $CO$-n jelzett $4\text{'}$ ponttal. $A4$ és $B4\text{'}$ egyenesek metszéspontja $M$. Ekkor $AE4▵\cong BO4\text{'}▵$; ugyanis ezen két derékszögű háromszög befogói egyenlők: $AE=BO$ és $E4=O4\text{'}$. Ebből következik, hogy $\begin{array}{c}{\displaystyle OB4\text{'}\sphericalangle =EB4\sphericalangle \mathrm{.}}\end{array}$ Már most $\begin{array}{c}{\displaystyle MAB\sphericalangle \equiv 4AB\sphericalangle ={90}^{\circ }-EA4\sphericalangle \mathrm{,}}\end{array}$ tehát $\begin{array}{c}{\displaystyle MAB\sphericalangle ={90}^{\circ }-OB4\text{'}\sphericalangle ={90}^{\circ }-ABM\sphericalangle \mathrm{,}}\end{array}$ vagyis $\begin{array}{c}{\displaystyle MAB\sphericalangle +ABM\sphericalangle ={90}^{\circ }}\end{array}$ és így $AMB\sphericalangle ={90}^{\circ }$, azaz $M$ pont az $AB$ átmérőjű körön fekszik.   b) Legyenek $AB$ és $CD$ egy ellipszis konjugált átmérői. Metszéspontjuk, $O$, az ellipszis középpontja. Ha $A$ pontban $CD$-vel, a $C$ pontban $AB$-vel húzunk párhuzamost, ezek az ellipszis érintői lesznek. E két érintő metszéspontja legyen $E$. A $CE$ és $CO$ vonaldarabokat beosztjuk $n$ egyenlő részre. 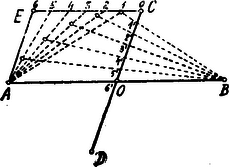    A $CE$ és $CO$ megfelelő osztópontjait összekötjük $A$-val, ill. $B$-vel. Az összekötő egyenesek metszéspontjai az ellipszis egy-egy pontját szolgáltatják. (Ábránkban $n=6$).   Pichler László (Zrínyi Miklós rg. VI. o. Bp. VIII.)