Kezdőlap


Feladat:	1000. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Apfel B. , B. Major P. , Barna T. , Cseh S. , Dénes P. , Feigl J. , Holzer P. , Kardos Gy. , Kerényi R. , Komlós J. , Kondor I. , Lóránd E. , Nagy E. , Németh K. , Radovics Gy. , Schreiber B. , Seidl G. , Somogyi Antal , Szél Gy. , Tarnóczy L.
Füzet:	1935/október, 38 - 39. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletrendszerek, Másodfokú (és arra visszavezethető) egyenletek, Derékszögű háromszögek geometriája, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1935/május: 1000. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen 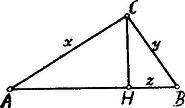$A C = x$ , $B C = y$ , $H B = z$ .

E három ismeretlenre nézve a következő három egyenlet áll fenn:

\begin{matrix} x^{2} + y^{2} & = c^{2}, & (1) \\ x + z & = k, & (2) \\ y^{2} & = c z . & (3) \end{matrix}

Az (1) a Pythagoras-tétel; (2) a feladat speciális követelménye; (3) az

y

befogóra alkalmazott Euklides-tétel.
(2)-ből

z = k - x

; ezt (3)-ba helyettesítve

y^{2} = c (k - x)

y^{2}

ezen kifejezését (1)-be helyettesítve

\begin{matrix} x^{2} + c (k - x) = c^{2} ill. x^{2} - c x + c (k - c) = 0. \end{matrix}

(4)

Taglalás. A (4) egyenlet

x

-re nézve két értéket szolgáltat; ezek megfelelnek, ha reális, pozitív értékek, azonban

c

-nél kisebbek; ugyanis

x

befogót jelent azon derékszögű háromszögben, melyben

c

átfogó. A (2) szerint

x < k

tartozik lenni. Minthogy azonban

A C > A H

A H + H B < A C + H B

, azaz

c < k

tartozik lenni; nyilván

x < k

, ha

x < c

.
A (4) gyökei valósak, ha

\begin{matrix} c^{2} - 4 c (k - c) > 0 ill. c (5 c - 4 k) \geq 0 azaz k \leq \frac{5 c}{4} . \end{matrix}

A (4) gyökeinek szorzata:

c (k - c) > 0

, hacsak

k > c

; a gyökök összege:

c

természetszerűleg pozitív. Tehát a (4) mindkét gyöke valós és pozitív, ha

c < k \leq \frac{5 c}{4}

. Minthogy a pozitív gyökök összege

c

, mindegyik

< c

, tehát mindegyik megfelel.
A feladatnak eszerint két megoldása van, ha

c < k \leq \frac{5 c}{4}

.
A

k = \frac{5 c}{4}

határesetben a két megoldás összeesik. Ekkor

\begin{matrix} x_{1} = x_{2} = \frac{c}{2} és y = \sqrt[]{c (\frac{5 c}{4} - \frac{c}{2})} = \frac{c}{2} \sqrt[]{3} . \end{matrix}

(A derékszögű háromszög hegyes szögei:

30^{\circ}

és

60^{\circ}

k = c

mellett

x = 0

, ill.

x = c

, azaz a háromszög az

A B

egyenes vonaldarabbá zsugorodik össze.

\begin{matrix} A (4) egyenletből & x = \frac{c + \sqrt[]{c (5 c - 4 k)}}{2}, \\ (2) alapján & z = k - x = \frac{2 k - [c \pm \sqrt[]{c (5 c - 4 k)}]}{2}, \\ (3) & y = \sqrt[]{c z} = \sqrt[]{\frac{c}{2} [2 k - c \pm \sqrt[]{c (5 c - 4 k)}]} . \end{matrix}

Somogyi Antal (Gyakorló középiskola V. o. Bp.)