Kezdőlap


Feladat:	955. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Barna Tibor , Cseh S. , Gilyén J. , Horovitz Kató , ifj. Jankovich I. , Kardos Gy. , Kemény György , Koch E. , Komlós János , Kondor I. , Kőnig L. , Németh K. , Radovics Gy. , Révész A. , Schreiber B. , Schuller I. , Schwarcz J. , Szabó O. , Szájbély J. , Szűcsi I. , Tárczy T. , Tarnóczy L. , Usarovits T. , Vargha T.
Füzet:	1935/február, 152 - 154. oldal		PDF \| MathML
Témakör(ök):	Alakzatok hasonlósága, Körérintési szerkesztések, Hiperbola, mint kúpszelet, Gyakorlat
Hivatkozás(ok):	Feladatok: 1934/december: 955. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Legyen az adott kör középpontja $O$ és a keresett kör középpontja $O'$ ; ezen pontnak azon $e$ egyenesen kell feküdnie, mely $a$ -ra az $A$ pontban merőleges. Az $O'$ kör az $O$ kört a $C$ pontban érintse. $C$ a két kör hasonlósági pontja. Ha $A C$ ez $O$ kört a $B$ pontban metszi, akkor $O B ∥ O' A$ , tehát $O B ⊥ a$ . Eszerint a $C$ pont azon egyenesen fekszik, amely az $A$ pontot összeköti az $O$ kör azon átmérőjének egyik végpontjával, amely merőleges $a$ -r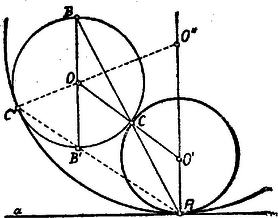a.

A szerkesztés menete tehát ez lesz: az

O

körnek az

a

egyenesre merőleges átmérőjének egyik végpontját,

B

összekötjük

A

-val.

A B

O

kört még a

C

pontban metszi. Az

A

pontban

a

-ra az

e

merőlegest állítjuk; az

O C

egyenes az

e

-t a keresett kör

O'

középpontban metszi.
Két megoldás van. (

O'

és

O''

középpontokkal: az egyiket kívülről a másikat belülről érinti az

O

kör. Más esetek is lehetségesek.)

Horovitz Kató (Ráskai Lea leánygimn. V. o. Bp. V.)

II. Megoldás. Legyen az adott kör középpontja

O

, sugara

r

. A keresett kör középpontja nyilván azon

e

egyenesen fekszik, amely

a

-ra az

A

pontban merőleges.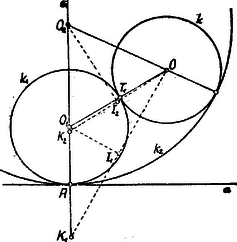

e

egyenesen keressük meg az

a

egyenesre nézve szimmetrikus

K_{1}

és

K_{2}

pontokat úgy, hogy

A K_{1} = A K_{2} = r

legyen. Az

O K_{1}

távolság

I_{1}

. ill. az

O K_{2}

, távolság

I_{2}

felezőpontjában az

O K_{1}

-re, ill.

O K_{2}

-re állított merőleges az

e

egyenest az

O_{1}

, ill.

O_{2}

pontban metszi.
Az

O_{1}

oly kör középpontja legyen, melynek sugara

r_{1} = O_{1} A

; ezen kör az

a

egyenest az

A

pontban érinti, az

O

kört pedig azért, mert

\begin{matrix} O O_{1} = K_{1} O_{1} = A K_{1} + A O_{1} = r + r_{1} . \end{matrix}

O_{2}

oly kör középpontja legyen, melynek sugara

r_{2} = O_{2} A

; ezen kör az

a

egyenest az

A

pontban érinti, az

O

kört pedig azért, mert

\begin{matrix} O O_{2} = K_{2} O_{2} = A O_{2} - A K_{2} = r_{2} - r . \end{matrix}

Komlós János (Széchenyi István gyakorló r. V. o. Pécs).

Jegyzet. Amint látjuk

\begin{matrix} O O_{1} - A O_{1} = r ill. A O_{2} - O O_{2} = r . \end{matrix}

Ez ennyit jelent, hogy az

O_{1}

, ill.

O_{2}

pontok oly hiperbolán feküsznek, melynek gyújtópontjai az

A

és

O

szilárd pontok és valós tengelye

= r

.
Ilyen értelemben mondhatjuk, hogy meg kell keresnünk a hiperbola és az

e

egyenes közös pontjait. Ezen feladat megoldását azonban csak úgy végezhetjük el, amit azt előbb megadtuk.

III. Megoldás. A keresett kör középpontjának az

e

egyenesen kell feküdnie.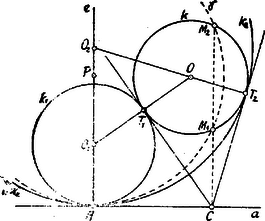

e

egyenes valamely

P

pontjából

P A

sugárral

γ

kört szerkesztünk, mely az

O

kört az

M_{1}

M_{2}

pontokban metszi. Az

M_{1} M_{2}

egyenes az

O

és

γ

körök hatványvonala, mely az

a

egyenest a

C

pontban metszi. Ezen

C

pont, az 1049. feladat szerint (l. ezen évf. 4. számában) az

O

körnek, továbbá az

a

egyenest

A

pontban érintő és az

O

kört metsző ill. érintő körök hatványvonalainak közös pontja. Húzzunk tehát a

C

pontból az

O

körhöz érintőket, melyeknek érintési pontjai

T_{1}

, ill.

T_{2}

. A keresett körök ezen pontokban érintik az

O

kört. Az

O T_{1}

ill.

O T_{2}

egyenes az

e

egyenest az

O_{1}

ill.

O_{2}

pontban metszi,

O_{1}

ill.

O_{2}

a keresett kör középpontja; sugara

O_{1} A

ill.

O_{2} A

Kemény György (Szent István rg. V. o. Bp. VII.)