Kezdőlap


Feladat:	934. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Barna T. , Baruch Z. , Blum Aranka , Czinczenheim J. , Földesi T. , Grózinger S. , Harsányi J. , Illovszky G. , Kálmán T. , Kapcsándi I. , Kardos Gy. , Keiner S. , Kerényi R. , Koch Ernő , Komlós J. , Kőnig L. , Lukács J. , Mezei S. , Pichler L. , Schwartz J. , Stachó L. , Wachsberger Gy. , Weiszfeld I. , Zádor Gy.
Füzet:	1934/december, 92. oldal		PDF \| MathML
Témakör(ök):	Beírt háromszög, Súlyvonal, Kör (és részhalmaza), mint mértani hely, Parabola, mint mértani hely, Gyakorlat
Hivatkozás(ok):	Feladatok: 1934/október: 934. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az adott körben, melynek középpontja $O$ , felmérjük a $B C = a$ húrt. Legyen adva a $B$ csúcsból kiinduló oldalfelező, $k_{b}$ . Az $A C$ oldal $D$ felezőpontja a $B$ körül $k_{b}$ sugárral rajzolt körön fekszik.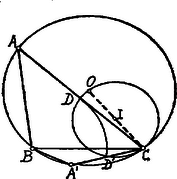

Másrészt a

C

ponton átmenő húrok felezőpontjai oly körön feküsznek, melynek átmérője

O C

, középpontja

I

. (Ugyanis

O D C ∢ = 90^{\circ}

; Thales tétele!) Eszerint a

D

pont az utóbbi két kör közös pontja; ilyen kettő van,

D

és

D'

. Ha már most

C D

O

adott kört az

A

pontban,

C D'

A'

pontban metszi, akkor

A B C

és

A' B C

a feltételeknek megfelelő háromszögek.
Ha a

k_{b}

sugarú kör az

O C

átmérőjű kört érinti, 1 megoldás van; ha e két körnek nincs közös pontja, nincs megoldás.

Koch Ernő (Br. Eötvös József r. VI. o. Bp. IV.)