Kezdőlap


Feladat:	892. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bálint J. , Brill György , Bukszbaum Gy. , Czinczenheim I. , Hegedűs J. , Kádár Gy. , Kálmán L. , Kapcsándi I. , Karner R. , Keiner S. , Kepes Á. , Magyar K. , Pick Gy. , Preszmayer K. , Székely L. , Villani F. , Wachsberger Gy.
Füzet:	1934/május, 256 - 257. oldal		PDF \| MathML
Témakör(ök):	Egyenlőtlenségek grafikus megoldása, Másodfokú (és arra visszavezethető) egyenlőtlenségek, Egyéb ponthalmazok a koordinátasíkon, Parabola, mint kúpszelet, Gyakorlat
Hivatkozás(ok):	Feladatok: 1934/március: 892. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egyenlőtlenségünket oly $x$ , $y$ értékpárok elégítik ki, amelyekkel

\begin{matrix} y - x^{2} + 4 x - 3 és x - y \end{matrix}

egyenlő előjelűek. Vizsgáljuk tehát ezen kifejezések előjelét; ezen célból megállapítjuk először, hogy mely

x

y

értékpároknál lesz

\begin{matrix} y - x^{2} + 4 x - 3 = 0 ill. y = x^{2} - 4 x + 3 \end{matrix}

(1)

és

\begin{matrix} x - y = 0 ill. y = x . \end{matrix}

(2)

Az (1) egyenletnek oly parabola felel meg, amelynek alsó tetőpontját

x = 2

y = - 1

koordináták határozzák meg az

X

-tengelyt

x_{1} = 1

és

x_{2} = 3

pontokban metszi. A parabola tengelye párhuzamos az

Y

-tengellyel. A sík azon pontjaira nézve, amelyek a parabolán belül vannak,

y > x^{2} - 4 x + 3

; a parabolán kívül fekvő pontokra pedig

y < x^{2} - 4 x + 3

.
A (2) egyenletnek egyenes felel meg, mely az origón megy keresztül és

45^{\circ}

-ú szög alatt hajlik az

X

-tengelyhez. A sík azon pontjaira nézve, melyek az egyenes fölött (az

Y

-tengely poz. részével együtt) feküsznek,

y > x

, azaz

x - y < 0

, az egyenes alatt fekvő pontokra nézve tehát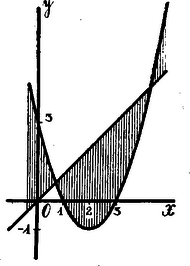

x - y > 0

Eszerint

\begin{matrix} y - x^{2} + 4 x - 3 > 0 és x - y > 0 \end{matrix}

egyidejűleg a sík azon pontjaira nézve, amelyek az egyenes által lemetszett parabolaszeleten belül feküsznek.
Továbbá:

\begin{matrix} y - x^{2} + 4 x - 3 < 0 és x - y < 0 \end{matrix}

a sík azon pontjaira vonatkozólag áll fenn egyidejűleg, amelyek a parabolán kívül és az egyenes fölött feküsznek.
Azon pontok, melyeknek

x

y

koordinátái kielégítik az egyenlőtlenséget, a sík vonalkázott részein feküsznek.

Brill György (Bolyai r. VI. o. Bp. V.).