Kezdőlap


Feladat:	866. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Apor Gy. , Brill Gy. , Buresch Margit , Hegedűs János , Hirschler Z. , Kádár Gy. , Kálmán László , Kepes Á. , Novák Ferenc , Preszmayer K. , Renner Z. , Surányi J. , Szele T. , Sziklai L.
Füzet:	1934/március, 191 - 192. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Síkgeometriai szerkesztések, Gyakorlat
Hivatkozás(ok):	Feladatok: 1933/december: 866. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. A kör $O$ középpontjából állítsunk merőlegest az $A C$ húrra; ennek talppontja legyen 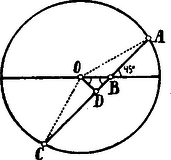$D$ .

Minthogy

O B D ∢ = B O D ∢ = 45^{\circ}

, az

O B D ▵

egyenlőszárú derékszögű háromszög:

O D = B D

. Most már

\begin{matrix} {\bar{A B}}^{2} + {\bar{B C}}^{2} = {(A D - B D)}^{2} + {(C D + B D)}^{2} = \\ = {(A D - O D)}^{2} + {(A D + O D)}^{2} = 2 ({\bar{A D}}^{2} + {\bar{O D}}^{2}) = \\ = 2 {\bar{A O}}^{2} = 2 r^{2} . \end{matrix}

Hegedűs János (Koháry István rg. VI. o. Gyöngyös.)

II Megoldás. Keressük meg a

C

pontnak az

O B

átmérőre vonatkozó szimmetrikus pontját,

C_{1}

-et; ez a körön fekszik.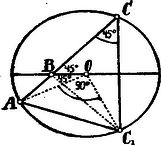

Ekkor

B C C_{1} ▵

egyenlő szárú, úgy hogy

B C_{1} = B C

; másrészt az

O B

-re való szimmetria miatt

B C_{1} ⊥ B C

és így

B C C_{1} ∢ = 45^{\circ}

. Ezen kerületi szög az

A C_{1}

ívhez tartozik, tehát a középponti

A O C_{1} ∢ = 90^{\circ}

. Már most

\begin{matrix} {\bar{A B}}^{2} + {\bar{B C}}^{2} = {\bar{A B}}^{2} + {\bar{B C}}_{1}^{2} = {\bar{A C}}_{1}^{2} \end{matrix}

azonban

\begin{matrix} {\bar{A C}}_{1}^{2} = {\bar{A O}}^{2} + {\bar{C_{1} O}}^{2} = 2 r^{2} . \end{matrix}

Kálmán László és Novák Ferenc (Mátyás Király rg. VI. o. Bp. II.)