Feladat: 855. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bálint J. ,  Brill Gy. ,  Csanádi Gy. ,  Czégé I. ,  Fodor I. ,  Hümpfner Olga ,  Jász L. ,  Kádár Gy. ,  Kálmán L. ,  Klein S. ,  Kovács Pál ,  Lusteiner Gy. ,  Novák F. ,  Pick Gy. ,  Preszmayer K. ,  Pulay M. ,  Schwertner M. ,  Surányi J. ,  Turda E. ,  Vass T. 
Füzet: 1934/január, 131 - 132. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek egybevágósága, Érintősokszögek, Gyakorlat
Hivatkozás(ok):Feladatok: 1933/november: 855. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek a sokszög egymás után következő csúcsai A, B, C, D, E úgy, hogy

AB=BC=CD=DE=...ésA^=B^=E^=...,ill.B^=D^=...

Húzzuk meg a B^ és C^ szögek felezőit; ezek egy O pontban metszik egymást, mely az AB, BC, CD oldalaktól egyenlő távolságban van, azaz oly kör középpontja, mely az AB, BC, CD oldalakat érinti.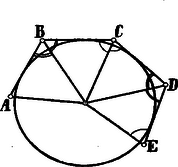
 
 

Minthogy CO felezi a C^ szöget és BC=CD, azért BCO▵≅DCO▵; ebből következik: OB=OD és CBO^=CDO^. Azonban CBO^ fele a B^-nek; így a CBO^-val egyenlő CDO^ is fele a B^-vel egyenlő D^-nek, tehát CDO^ is fele a D^-nek. Minthogy DE=CD, OD=OD és ODE^=ODC^, következik: ODE▵≅ODC▵ és ezért egyenlő oldalaikhoz, CD- és DE-hez egyenlő magasságok tartoznak; más szóval: a fenti O kör DE-t is érinti.
Látjuk tehát, hogy azon kör, mely a sokszög három egymás után következő oldalát érinti, érinti a negyediket is és í. t. valamennyit.
 

Kovács Pál (Premontrei g. VII. o. Szombathely)