Kezdőlap


Feladat:	845. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bálint J. , Brill Gy. , Bródy Éva , Gyopár L. , Hirschler Z. , Kádár Gy. , Kálmán L. , Kepes Á. , Klein S. , Novák F. , Pick Gy. , Preszmayer K. , Renner Z. , Schiff Erzsébet , Surányi J. , Székely I. , Waschberger György , Weiszfeld István
Füzet:	1933/december, 96. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Beírt alakzatok, Egyenlő szárú háromszögek geometriája, Húrsokszögek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1933/október: 845. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Tekintsük a sokszög három egymásután következő $A_{1} A_{2}$ , $A_{2} A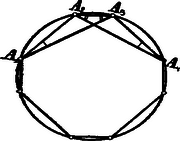_{3}$ , $A_{3} A_{4}$ oldalát.

Feltevésünk szerint

A_{1} A_{2} A_{3} ∢ = A_{2} A_{3} A_{4} ∢

.
Másrészt

A_{2} A_{1} A_{3} ∢ = A_{2} A_{4} A_{3} ∢

, minthogy a közös

\hat{A_{2} A_{3}}

íven álló kerületi szögek. Eszerint az

A_{1} A_{2} A_{3} Δ

és

A_{2} A_{3} A_{4} Δ

két szöge egyenlő; ebből következik:

A_{2} A_{3} A_{1} ∢ = A_{3} A_{2} A_{4} ∢

. Ezen kerületi szögekhez tehát egyenlő húrok tartoznak:

A_{1} A_{2} = A_{3} A_{4}

s. í. t.

Weiszfeld István (Kemény Zsigmond r. V. o. Bp. VI.)

II. Megoldás. Kössük össze a kör

O

középpontját az

A_{1}

A_{2}

A_{3}

A_{4}

, csúcsokkal. Minthogy

A_{2} A_{3} O Δ

egyenlő szárú háromszög, az

A_{2} A_{3}

alapon fekvő szögek egyenlőek; ha ezeket az egyenlő

A_{1} A_{2} A_{3} ∢

és

A_{2} A_{3} A_{4} ∢

szögekből kivonjuk, a különbségek is egyenlők, azaz

A_{1} A_{2} O ∢ = A_{4} A_{3} O ∢

. Ebből következik, hogy

A_{1} A_{2} O Δ ≅ A_{3} A_{4} O Δ

és így

A_{1} A_{2} = A_{3} A_{4}

Wachsberger György (Izr. rg. V. o. Bp.)

Jegyzet. Lényegileg: az

A_{1} A_{2} A_{3} A_{4}

törtvonal szimmetriatengelye a körnek

A_{2} A_{3}

-ra merőleges átmérője.
A feltételeknek megfelelő idom a legegyszerűbb esetben

(2 n = 4)

a téglalap.