Feladat: 823. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Brill Gy. ,  Buresch Margit ,  Csanádi Gy. ,  Csurgói ref. rg. VI. o. ,  Czégé I. ,  Faragó P. ,  Fenyő I. ,  Fischmann Éva ,  Hümpfner Olga ,  Jachja L. ,  Janits I. ,  Jász L. ,  Paál S. ,  Pick Gy ,  Porges A. ,  Rott Miklós ,  Schwertner M. ,  Singer I. ,  Steiner Z. ,  Szele T. ,  Sziklai M. ,  Verebély L. 
Füzet: 1933/október, 36 - 37. oldal  PDF  |  MathML 
Témakör(ök): Beírt alakzatok, Húrnégyszögek, Diszkusszió, Négyszögek szerkesztése, Gyakorlat
Hivatkozás(ok):Feladatok: 1933/május: 823. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az adott k körben tetszőleges helyzetben felvesszük az átlókkal egyenlő AC és EF húrokat. A k körrel koncentrikus k' kört szerkesztünk, amely az EF húrt érintse és pl. az O középponton át meghúzzuk az OX egyenest, mely AC-vel az átlók szögével egyenlő szöget zár be. Már most a k' körhöz az OX egyenessel párhuzamos érintőt húzunk. Ennek az érintőnek a k körben fekvő darabja lesz a négyszög BD átlója. BD=EF, mert a k körnek a középponttól egyenlő távolságban fekvő húrjai. Az A, B, C, D pontok a keresett négyszög csúcsai.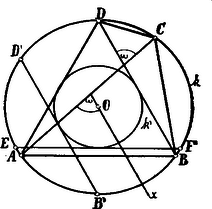

 
 

Minthogy a k' körhöz az OX egyenessel párhuzamosan két érintő húzható, a megoldások száma: 2, 1, 0. Hogy a négyszög létezzék, szükséges, hogy BD ill. B'D' az AC-t a körön belül messe.
 

Rott Miklós (Birodalmi német rg. VI. o. Bp.)
 

Jegyzet. Az átlóknak van egy hegyes és egy tompa szögük; a szerkesztésnél, bár nem kifejezetten, a hegyes szöget (ω) vettük tekintetbe. Felmerül a kérdés, mekkorának kell ennek lennie, hogy a k' kör BD érintője az AC-t a körön belül messe?
Legyen AC>BD. Az AC húr egyik végpontjából a BD-vel, mint sugárral kört szerkesztünk; ez a k kört két pontban metszi, azaz a hosszabbik húr egyik végpontjából kétféleképpen jelölhetjük ki a kisebbik húrt. Ilyen módon az AC-vel a BD hosszú húrok két különböző szöget zárnak be: φ1-t és φ2-t. Legyen φ1<φ2. Ha már most az átlók szöge, ω≦φ1, akkor nincs megoldás. Ha φ1<ω≦φ2, egy megoldás van; ha φ2<ω, két megoldás.