Kezdőlap


Feladat:	812. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bauer Gy. , Bayer M. , Brill Gy. , Csanádi Gy. , Csurgói ref. rg. VI. o. , Czetz S. , Darvasy M. , Faragó P. , Fenyő I. , Fischmann Éva , Füves I. , Huber Margit , Janits I. , Jász L. , Kellner O. , Kovács P. , Krausz J,. , Kürthy Ö. , Lukács L. , Nagy E. , Paál S. , Pestál A. , Pick Gy. , Polyóka L , Porges A. , Pulay M. , Róth Alice , Sándor Miklós , Schwertner M. , Steiner Z. , Szele T. , Thezarovich E. , Turda E. , Varga Z. , Vass T. , Verebély L.
Füzet:	1933/szeptember, 6 - 7. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Numerikus és grafikus módszerek, Terület, felszín, Térgeometriai számítások trigonometria nélkül, Gyakorlat
Hivatkozás(ok):	Feladatok: 1933/április: 812. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . Legyen $M$ a $B C$ oldal felezőpontja; $B M = M C = 6$ .

\begin{matrix} \bar{A M^{2}} = 12^{2} - 6^{2} = 108; \bar{D M^{2}} = \bar{A D^{2}} + \bar{A M^{2}} = 25 + 108 = 133. \end{matrix}

D M

B C D

egyenlőszárú háromszög magassági vonala, a

B C

alapra vonatkozólag. A

B C D ▵

területe

\begin{matrix} t = \frac{1}{2} \bar{B C} \cdot \bar{D M} = 6 \sqrt[]{133} \approx 69, 1953 {cm}^{2} = 6919, 53^{m} /_{m^{2}} . \end{matrix}

Eszerint

1^{m} /_{m^{2}}

pontossággal

t = 6920^{m} /_{m^{2}}

2^{\circ}

. Az

A B C ▵

köré írt kör

O

középpontjában emeljünk merőlegest az

A B C

síkra; ezen

e

merőleges minden pontja egyenlő távolságban van az

A

B

C

pontoktól.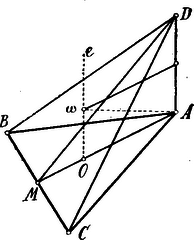

e ∥ A D

és így ezen két egyenesen át síkot fektetünk; ezen síkban megszerkesztjük az

A D

távolságot merőlegesen felező egyenest mely

e

-t az

ω

pontban metszi. Most már

ω

egyenlő távolságban van

A

-tól és

D

-től, tehát az

A

B

C

D

pontoktól; eszerint

ω

e négy pont által meghatározott gömb középpontja. E gömb egyik sugara

ω A = R

és

\begin{matrix} R^{2} = \bar{ω O^{2}} + \bar{A O^{2}} = {(\frac{A D}{2})}^{2} + {(\frac{2}{3} A M)}^{2}; \\ R^{2} = \frac{25}{4} + \frac{4}{9} 108 = \frac{25}{4} + 48 = \frac{217}{4}; \\ R = \frac{1}{2} \sqrt[]{217} \approx 7, 36 cm, \end{matrix}

azaz

1^{m} /_{m}

pontossággal

R = 74^{m} /_{m}

Sándor Miklós (Faludi Ferenc rg. VI. o. Szombathely)

Jegyzet: A megoldások között többen nem vették figyelembe azon követelményt, mely a számítás pontosságára vonatkozik. Így pl. az

1^{\circ}

. alatti területszámításnál

\sqrt[]{133}

közelítő értékét a 6-tal való szorzás miatt legalább is tízezredrész pontosságig kell számítani.
Az egyes pontossággal meghatározandó értéket úgy kell megállapítanunk, hogy a hiba 0,5-nél ne legyen nagyobb. Ezért mind a két esetben,

1^{\circ}

. és

2^{\circ}

. alatt is a fölösen közelítő értéket kellett vennünk.