Kezdőlap


Feladat:	803. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Csanádi Gy. , Fenyő I. , Füves I. , Hümpfner Olga , Janits I. , Jász L. , Lukács P , Pick Gy. , Rachl T. , Steiner Z. , Szele Tibor , Verebély L.
Füzet:	1933/május, 255. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Súlyvonal, Terület, felszín, Párhuzamos szelők tétele, Gyakorlat
Hivatkozás(ok):	Feladatok: 1933/március: 803. matematika gyakorlat

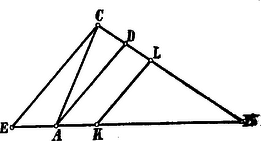
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha a megadott irány a háromszög valamely súlyvonalának (oldalfelező transzverzális) irányával megegyező, akkor az illető súlyvonal lesz azon egyenes, mely a háromszög területét felezi.
Az előbbi esetet most már kizárva, húzzunk a háromszög három csúcsán át a megadott irányban párhuzamosakat; ezek közül csak egy lesz, mely a háromszöget két részre hasítja; legyen ez $A D$ .

Ha az

A B D ▵

területe nagyobb, mint az

A C D ▵

-é, akkor a keresett egyenes az

A B D ▵

-et szeli; tegyük fel, hogy ezen szelő

K L (∥ A D)

, azaz a

B K L ▵

területe az

A B C ▵

-ének a fele. Minthogy e két háromszögnek egy közös szöge van, területük úgy aránylik egymáshoz, mint az egyenlő szögeket bezáró oldalak szorzata és így

\begin{matrix} \bar{B K} \cdot \bar{B L} = \frac{\bar{B A} \cdot \bar{B C}}{2} . \end{matrix}

(1)

Azonban

\begin{matrix} B K : B L = B A : B D, \end{matrix}

(2)

tehát

\begin{matrix} {\bar{B K}}^{2} = \frac{{\bar{B A}}^{2} \cdot \bar{B C}}{2 B D} . \end{matrix}

(3)

Ezen eredményt a következő alakban írhatjuk:

\begin{matrix} B K = \frac{B A \cdot B C}{B D} = \frac{B A}{2} : B K . \end{matrix}

(4)

Legyen

C E ∥ A D

; ekkor

\begin{matrix} B E : B A = B C : B D azaz B E = \frac{B A \cdot B C}{B D}, \end{matrix}

tehát

\begin{matrix} B K : B E = \frac{B A}{2} : B K, \end{matrix}

azaz

B K

B E

és

\frac{1}{2} B A

távolságok mértani középarányosa és így

B K

megszerkeszthető. A

K

ponton át az adott irányban (

∥ A D

) szelőt húzunk, mely a követelményt kielégíti.

Szele Tibor (Ref. rg. V. o. Debrecen)