Kezdőlap


Feladat:	762. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Adler Gy. , Blahovits Gy. , Bodó L. , Faragó P. , Jász L. , Kratky J. , Ottinger Gy. , Pick Gy. , Rachl T. , Róth Gy. , Semtei J. , Varga Z. , Verebély László
Füzet:	1933/január, 129 - 130. oldal		PDF \| MathML
Témakör(ök):	Súlyvonal, Kör (és részhalmaza), mint mértani hely, Párhuzamos szelők tétele, Háromszögek szerkesztése, Parabola, mint mértani hely, Gyakorlat
Hivatkozás(ok):	Feladatok: 1932/november: 762. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $A B C$ a keresett háromszög, melynek adott oldalai $A C$ és $B C$ ; súlyvonalai, $A A_{1}$ és $B B_{1}$ az $S$ pontban metszi egymást. Húzzunk $B_{1}$ -ből az $A A_{1}$ -gyel párhuzamost, mely $B C$ oldalt a $D$ -pontban metszi.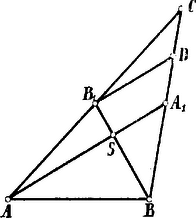

Ekkor

\begin{matrix} C D : C A_{1} = C B_{1} : C A, azaz C D : \frac{a}{2} = 1 : 2, tehát C D = \frac{a}{4}; B D = \frac{3 a}{4} . \end{matrix}

A A_{1} ⊥ B B_{1}

, akkor

B_{1} D ⊥ B B_{1}

, azaz a

B_{1}

pont a

B D

átmérő felett rajzolt félkörön fekszik.
Ezek szerint a szerkesztés: tetszőleges egyenesre rámérjük a

B A_{1} = A_{1} C = \frac{a}{2}

darabokat és kijelöljük az

A_{1} C

felezési pontját,

D

-t. Ezután

B D

mint átmérő fölé félkört rajzolunk; ezt a

C

körül

\frac{a}{2}

sugárral vont kör a

B_{1}

-ben metszi.

C B_{1}

meghosszabbítására felmérjük a

B_{1} A = C B_{1}

távolságot;

A B C

lesz a keresett háromszög.
Ennek két oldala valóban megadott

a

és

b

hosszúságok: csak azt kell még bizonyítanunk, hogy

A A_{1} ⊥ B B_{1}

.
Szerkesztés szerint,

\begin{matrix} B A_{1} : B D = \frac{a}{2} : \frac{3 a}{4} = 2 : 3. \end{matrix}

A súlyvonalak tulajdonságából folyik:

\begin{matrix} B S : B B_{1} = 2 : 3. \end{matrix}

Egybevetve ezen két aránypárt:

\begin{matrix} B S : B B_{1} = B A_{1} : B D, \end{matrix}

amiért

B_{1} D ∥ S A_{1} \equiv A A_{1}

. De

B_{1} D ⊥ B B_{1}

és így

A A_{1} ⊥ B B_{1}

Verebély László (Kegyesrendi g. VI. o. Bp.)

Jegyzet: A szerkesztés lehetséges, ha a

C

körül

\frac{b}{2}

sugárral vont kör metszi a

B D

átmérő fölé szerkesztett félkört, tehát, ha

\begin{matrix} a > \frac{b}{2} > \frac{a}{4}, azaz 2 a > b > \frac{a}{2} . \end{matrix}

Ezt még úgy is kifejezhetjük, hogy az

a

és

b

oldalak bármelyike a másik felénél nagyobb tartozik lenni.