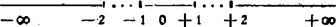Kezdőlap


Feladat:	726. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Baneth L. , Brill Gy. , Csanádi György , Deutsch E. , Döring A. , Erőd J. , Hümpfner Olga , Jachja L. , Kepes Á. , Lukács O. , Papp G. , Pulay M. , Semadam E. és K. , Singer G. , Singer I. , Spitz M. B. , Szakos Gy.
Füzet:	1932/október, 31. oldal		PDF \| MathML
Témakör(ök):	Abszolútértékes egyenlőtlenségek, Másodfokú (és arra visszavezethető) egyenlőtlenségek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1932/május: 726. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$x^{2} - 4$ és $x^{2} - 1$ egyenlő előjelűek tartoznak lenni.
a) $x^{2} - 4 > 0$ , ha $| x | > 2$ ; $x^{2} - 1 > 0$ , ha $| x | > 1$ . Összeegyeztetve e két feltételt, az egyenlőtlenség fennáll, ha $| x | > 2$ ; azaz $x > 2$ vagy $x < - 2$ .
b) $x^{2} - 4 < 0$ , ha, $| x | < 2$ és $x^{2} - 1 < 0$ , ha $| x | < 1$ . Összeegyeztetve e két feltételt, kell, hogy $| x | < 1$ legyen, azaz $- 1 < x < + 1$ .

A számvonal kihúzott részén fekvő pontokhoz tartozó

x

értékek felelnek meg a követelménynek; a pontozott részek nem felelnek meg.

Csanádi György (Kölcsey Ferenc rg. V. o. Bp. VI.)