Feladat:	717. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Aigner Sándor ,  Asztalos E. ,  Baneth L. ,  Bauer Gy. ,  Brill Gy. ,  Böhm Anna ,  Czégé I. ,  Deutsch E. ,  Döring A. ,  Feldmann J. ,  Fodor J. ,  Hümpfner Olga ,  Jachja L. ,  Jász L. ,  Lukács O. ,  Pulay M. ,  Róth Gy. ,  Singer I. ,  Spitz M. B. ,  Szabó G. ,  Weiszfeld E. ,  Ökrös J.
Füzet:	1932/szeptember, 6 - 7. oldal		PDF  |  MathML
Témakör(ök):	Egyenletek grafikus megoldása, Másodfokú (és arra visszavezethető) egyenletek, Gyökös függvények, Gyakorlat
Hivatkozás(ok):	Feladatok: 1932/április: 717. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.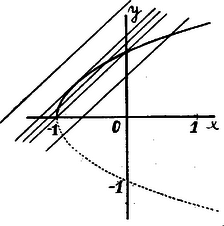   Az ${y=\left(x+1\right)}^{\frac{1}{2}}$ görbének és az $y=x+b$ egyenesnek közös pontja oly $x$ értékhez tartozik, amelynél $\begin{array}{c}{\displaystyle {\left(x+1\right)}^{\frac{1}{2}}=x+b\mathrm{,}}\end{array}$ (1) ill. $\begin{array}{c}{\displaystyle x+1={\left(x+b\right)}^2\mathrm{.}}\end{array}$ (2) Utóbbi egyenletet rendezve, az $\begin{array}{c}{\displaystyle x^2+\left(2b-1\right)x+b^2-1=0}\end{array}$ (3) egyenlethez jutunk. Hogy a görbének és az egyenesnek közös pontja legyen, szükséges, hogy a (3) egyenlet gyökei valósak legyenek; ennek pedig a feltétele: $\begin{array}{c}{\displaystyle {\left(2b-1\right)}^2-4\left(b^2-1\right)\ge \mathrm{0,}\text{<span style="font-weight: normal;font-style: normal;">azaz</span>}b\le \frac{5}{4}\mathrm{.}}\end{array}$ Ha $b=\frac{5}{4}$, akkor a (3) egyenletnek két, egyenlő valós gyöke van; az $\begin{array}{c}{\displaystyle x^2+\frac{3}{2}x+\frac{9}{16}=0\text{<span style="font-weight: normal;font-style: normal;">egyenlet gyökei:</span>}{x}_1=x_2=-\frac{3}{4}\mathrm{.}}\end{array}$ Az $y=x+\frac{5}{4}$ egyenes a görbét érinti az $x=-\frac{3}{4}$ pontban. Ha $b<\frac{5}{4}$, az egyenes az $y^2=x+1$ parabolát két pontban metszi; azonban $y={\left(x+1\right)}^{\frac{1}{2}}$ a parabolának csak az $X$-tengely felett fekvő részét jelenti és ezt az az $y=x+b$ egyenes két pontban metszi, amíg $1\le b\le \frac{5}{4}$. $b=1$ mellett a (3) gyökei: $x_1=-1$, $x_2=0$. Ha $b<1$, akkor az $y=x+b$ egyenes a parabola $X$-tengely feletti részét már csak egy pontban metszi.   Jegyzet. Az (1) egyenlet azt mutatja, hogy mivel ${\left(x+1\right)}^{\frac{1}{2}}\ge 0$, azért $x+b\ge 0$. A (3) egyenletnek tehát csak azon $x$ gyöke jöhet tekintetbe, amelyre nézve $x+b\ge 0$, azaz $x\ge -b$. Azt kell tehát megvizsgálnunk, hogy a (3) egyenletnek hány gyöke van $-b$ és $+\infty$ között. Ha $\begin{array}{c}{\displaystyle f\left(x\right)=x^2+\left(2b-1\right)x+b^2-\mathrm{1,}}\end{array}$ akkor $\begin{array}{c}{\displaystyle f\left(-b\right)=b-1\text{<span style="font-weight: normal;font-style: normal;">és</span>}f\left(+\infty \right)=+\infty \mathrm{.}}\end{array}$ Ebből láthatjuk hogy, ha $b<1$, akkor $f\left(-b\right)<0$, tehát $-b$ és $+\infty$ között a (3) egyenletnek csak egy gyöke van.