Feladat: 708. matematika gyakorlat Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Aigner S. ,  Baneth László ,  Bauer Gy. ,  Boor K. ,  Brambring V. ,  Brügler B. ,  Böhm Anna ,  Cristofoli V. ,  Czégé I. ,  Deutsch E. ,  Erdős Gy. (Bolyai) ,  Fejes Gy. ,  Fodor J. ,  Hümpfner Olga ,  Jász L. ,  Karsay S. ,  Kurz F. ,  Lukács O. ,  Lukács P. ,  Papp G. ,  Papp S. ,  Pikler F. ,  Pintér Gy. ,  Pulay M. ,  Róth Gy. ,  Sándor M. ,  Singer G. ,  Singer I. ,  Spitz M. ,  Szabó G. ,  Szakos Gy. ,  Takács V. ,  Taskó Gy. ,  Vozáry P. ,  Wagner W. ,  Weiszfeld E. ,  Zoldán E. ,  Ökrös J. 
Füzet: 1932/május, 255. oldal  PDF  |  MathML 
Témakör(ök): Másodfokú (és arra visszavezethető) egyenletek, Egyenesek egyenlete, Hiperbola egyenlete, Gyakorlat
Hivatkozás(ok):Feladatok: 1932/március: 708. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az y=1x függvénynek egyenlőszárú hiperbola felel meg, melynek aszimptotái a koordinátatengelyek; a görbe ágai az első és harmadik síknegyedben feküsznek.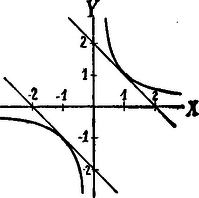
Az y=-x+b egyenes az X-tengelyhez 135∘ (ill. -45∘) alatt hajlik. b értékét változtatva párhuzamos egyeneseket kapunk, amelyek az Y tengelyt az x=0, y=b pontban metszik. Ezen egyenesek között vannak, amelyek a hiperbolát metszik (2 pontban); kettő van közöttük érintő, de az érintők között fekvő, velük párhuzamos egyenesek a hiperbolát nem metszik.

 
 

Hogy a közös pontok abscissáit megkapjuk, meg kell oldanunk, az
1x=-x+b.ill.x2-bx+1=0
egyenletet. Ennek gyökei jelentik a metszésportok abscissáit, melyek valósak, ha
b2-4≧0,azaz|b|≧2.

Ha b=±2, akkor egyenletünknek két egyenlő gyöke van, az egyenes két összeeső pontban metszi a hiperbolát, tehát érintővé válik.
Ha b>2 vagy b<-2, akkor az egyenes két pontban metszi a hiperbolát.
Ha -2<b<2, akkor az egyenes nem metszi a hiperbolát.
 

Baneth László (Verbőczy István rg. VI. o. Bp. I.)