Kezdőlap


Feladat:	698. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Abonyi A. , Aigner S. , Baneth L. , Bauer Gy. , Birkás I. , Böhm Anna , Csurgói ref. rg. V. , Czégé I. , Deutsch E. , Elek J. , Fejér I. , Győri I. , Hümpfner Olga , Jász L. , Kaiser F. , Kapui K. , Karsay S. , László P. , Lukács O. , Lukács P. , Németh I. , Papp G. , Paskusz J. , Pestál A. , Pikler F. , Pintér Gy. , Pulay M. , Róth G. , Rudas K. , Salusinszky I. , Singer I. , Singer O. , Spitz M. , Taskó Gy. , Vozáry Pál , Weisz D. , Weiszfeld E. , Ökrös J.
Füzet:	1932/április, 213 - 214. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Parabola egyenlete, Kúpszeletek érintői, Gyakorlat
Hivatkozás(ok):	Feladatok: 1932/február: 698. matematika gyakorlat

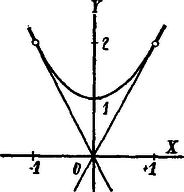
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $y = x^{2} + 1$ függvénynek oly parabola felel meg, melynek tengelye az $Y$ -tengely és alsó tetőpontjának koordinátái: $x = 0$ , $y = 1$ .
Az $y = m x$ a koordinátarendszer kezdőpontján áthaladó tetszőleges egyenest jelent. Ezen egyenes a parabolát oly pontban metszi, amelynek abscissája kielégíti az

\begin{matrix} x^{2} + 1 = m x, ill. x^{2} - m x + 1 = 0 \end{matrix}

egyenletet. Innen:

\begin{matrix} x = \frac{m \pm \sqrt[]{m^{2} - 4}}{2}, \end{matrix}

tehát

\begin{matrix} y = \frac{m}{2} (m \pm \sqrt[]{m^{2} - 4}) . \end{matrix}

Metszéspont valóban létezik, mégpedig kettő, ha

x

valós szám, azaz ha

\begin{matrix} m^{2} - 4 \geq 0, m^{2} \geq 4, ∣ m ∣ \geq 2. \end{matrix}

m = \pm 2

, akkor a két metszéspont összeesik; az

\begin{matrix} y = 2 x és y = - 2 x \end{matrix}

egyenesek a görbe érintői. Ezen érintők az

Y

-tengelyre nézve szimmetrikus helyzetűek. Mindazon egyenesek, amelyekre nézve

∣ m ∣ > 2

, az

y = 2 x

és az

Y

-tengely, továbbá az

y = - 2 x

és az

Y

-tengely közötti síkrészben feküsznek.

Vozáry Pál (Klauzál Gábor rg. V. o. Szeged.)