Kezdőlap


Feladat:	689. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Baneth László , Birkás J. , Csurgói ref. rg. V. o. , Deutsch E. , Engvel L. , Erdős Gy. (Bolyai) , Jász L. , Kaiser F. , Kajos J. , Kapui K. , Karsay S. , Kurz F. , Papp G. , Pimper Á. , Pintér Gy. , Róth Gy. , Széll G.. , Weisz D. , Weiszfeld E. , Widder Magda , Zsenaty Emilia
Füzet:	1932/március, 184 - 185. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Gyakorlat
Hivatkozás(ok):	Feladatok: 1932/január: 689. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.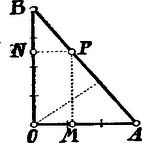

Legyen

O M = P N = x

a független változó. Minthogy

A P M ▵ \sim A B O ▵

\begin{matrix} P M : O B = M A : O A vagyis P M : b = (a - x) : a, \end{matrix}

tehát

\begin{matrix} P M = \frac{b (a - x)}{a}, \end{matrix}

és így

y = {\bar{P M}}^{2} + {\bar{P N}}^{2} = x^{2} + \frac{b^{2} {(a - x)}^{2}}{a^{2}} = \frac{1}{a^{2}} [(a^{2} + b^{2}) x^{2} - 2 a b^{2} x + a^{2} b^{2}]

x

érteke változik 0-tól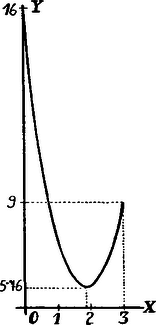

a

-ig.

\begin{matrix} Ha x = 0, y = b^{2}; ha x = a, \\ y = \frac{1}{a^{2}} [(a^{2} + b^{2}) a^{2} - 2 a^{2} b^{2} + a^{2} b^{2}] = a^{2} . \end{matrix}

A függvénynek minimuma van, ha

\begin{matrix} x = \frac{a b^{2}}{a^{2} + b^{2}} \\ és y_{min} = \frac{1}{a^{2}} [\frac{4 (a^{2} + b^{2}) a^{2} b^{2} - 4 a^{2} b^{4}}{4 (a^{2} + b^{2})}] = \\ = \frac{a^{2} b^{2}}{a^{2} + b^{2}} = {(\frac{a b}{c})}^{2}, \end{matrix}

ha t. i.

{\bar{A B}}^{2} = a^{2} + b^{2} = c^{2}

. Azonban

\frac{a b}{c}

nem egyéb, mint az

A O B ▵

átfogójához tartozó magasság.
Eszerint, miközben a

P

pont

B

-től

A

-ig mozog, a

{\bar{P M}}^{2} + {\bar{P N}}^{2}

összeg

b^{2}

-től csökken az

{(\frac{a b}{c})}^{2}

értékig és innen növekedik

a^{2}

-ig.
A megadott numerikus értékekkel

\begin{matrix} y = \frac{25}{9} x^{2} - x^{2} - \frac{96}{9} x + 16. \end{matrix}

Ezen függvény változását a köv. táblázat jellemzi:

\begin{matrix} x & 0 & 0,3 & 0,6 & 0,9 & 1 & 1,5 & 1,92 & 2 & 2,4 & 2,7 & 3 \\ y & 16 & 13,05 & 10,6 & 8,65 & 8,1 & 6,25 & 5,76 & 5,8 & 6,4 & 7,45 & 9 \\ min \end{matrix}

Baneth László (Verbőczi István rg. VI. o. Bp. I.).