Kezdőlap


Feladat:	652. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Baneth L. , Birkás J. , Böhm Annus , Dátán V. , Deutsch E. , Ehrlich János , Engel L. , Erdélyi Klára , Fejér I. , Jász L. , Kaiser F. , Kajos J. , Karsay S. , Kertész F. , Lukács O. , Mayer H. , Nemes Ö. , Németh J. , Pánczél D. , Papp G. , Papp S. , Paskusz J. , Pimper Á. , Pintér Gy. , Pulay M. , Róth Gy. , Róth Sára , Rumi J. , Schlesinger M. , Semadam E. és K. , Singer G. , Singer I. , Széll G. , Weisz D. , Weiszfeld E.
Füzet:	1931/november, 63 - 64. oldal		PDF \| MathML
Témakör(ök):	Rombuszok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1931/szeptember: 652. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . Minthogy $O_{1} A = O_{2} A = O_{1} B = O_{2} B = r$ , az $A O_{1} B O_{2}$ idom rombus. Ennek $O_{1} O_{2}$ átlója egyenlő a rombus oldalaival; ezért $A O_{1} O_{2} ▵$ egyenlő oldalú, tehát 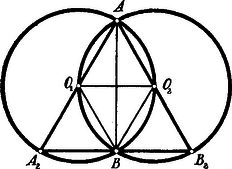$O_{1} A O_{2} ∢ = 60^{\circ}$ .

2^{\circ}

. Az

A B A_{1} ∢ = 90^{\circ}

, mert oly kerületi szög (az

O_{1}

körben), melynek szárai az

A A_{1}

átmérő végpontjain mennek keresztül. Hasonló okból

A B A_{2} ∢ = 90^{\circ}

. Mivel így

\begin{matrix} A B A_{1} ∢ + A B A_{2} ∢ = 180^{\circ}, \end{matrix}

A_{1}

B

A_{2}

pontok egy egyenesen feküsznek.

3^{\circ}

A A_{1} = A A_{2} = 2 r

és amint

1^{0}

alatt láttuk,

A_{1} A A_{2} ∢ = 60^{\circ}

; eszerint az

A A_{1} A_{2} ▵

is egyenlő oldalú.

Ehrlich János (Koháry István rg. VI. o. Gyöngyös)