| Feladat: | 619. matematika gyakorlat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Buresch R. , Böhm Anna , Deutsch E. , Kreutzer E. , Mayer Gy. , Megyery E. , Neumann K. , Paskusz S. , Réffy K. , Róth György , Singer I , Sohr Anna , Szabó I. , Weiszfeld E. | ||
| Füzet: | 1931/május, 275 - 276. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Síkgeometriai számítások trigonometria nélkül négyszögekben, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1931/március: 619. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Ismeretes, hogy egy négyszög oldalainak felező pontjai egy paralelogramma csúcsai; ezen paralelogramma oldalai párhuzamosak a négyszög átlóival. Szükséges tehát, hogy a megadott négy pont egy paralelogramma csúcsa legyen. 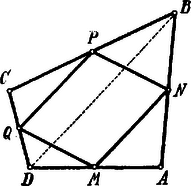 Tegyük fel, hogy az , , , pontok valóban egy paralelogramma csúcsai. Húzzunk az ponton keresztül tetszésszerinti egyenest és mérjük fel rá az távolságokat; ezután az egyenesre az , a egyenesre a távolságot mérjük fel. Így az négyszöghöz jutunk, melynek , , oldalait felezik rendre az , , pontok. Minthogy és , továbbá , azért és ; így egyenes a pontban felezi a oldalt. Az egyenes irányát és az távolságot tetszőlegesen választottuk, tehát valóban végtelen sok négyszöget szerkeszthetünk, mely a követelménynek megfelel. (Kettős határozatlanság!) Ezen négyszögek között csak egy paralelogramma van, t. i. amelynek oldalai az és egyenesekkel párhuzamosak. Trapéz végtelen sok van közöttük. Pl. legyen ; ekkor . ( a trapéz középvonala.)
|