Kezdőlap


Feladat:	555. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Deutsch E. , Fleischmann S. , Kiss J. , Láng Géza , Lemberger P. , Paskusz S. , Rolich A. , Rosta F. , Schlesinger E. , Singer I. , Sohr Anna , Szabó I. , Szoyka P. , Weiszfeld E.
Füzet:	1930/november, 78. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Síkgeometriai számítások trigonometria nélkül körökben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1930/szeptember: 555. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

$1^{\circ}$ . Az $A B$ , mint húr fölött szerkesztett kör a $B C$ átfogót csak a $B$ pontban érintheti; ezen kör középpontja, $O_{1}$ egyrészt az $A B$ -t merőlegesen felező egyenesen, másrészt a $B C$ -re a $B$ pontban emelt merőlegesen tartozik feküdni. Az $A B$ -t merőlegesen felező egyenes keresztül megy a $B C$ átfogó $O$ középpontján.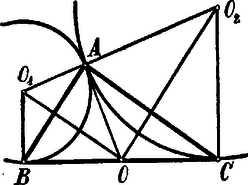

A másik kör középpontja

O_{2}

, az

A C

-t merőlegesen felező egyenes és a

B C

-re, a

C

pontban emelt merőleges közös pontja; az előbbi szintén keresztülmegy az

O

ponton.
Minthogy

O A = \frac{B C}{2} = O B

és

O_{1} A = O_{1} B

, továbbá

O_{1} O = O_{1} O

, következik, hogy

O_{1} A O ▵ ≅ O_{1} B O ▵

, tehát

O_{1} A O ∢ = O_{1} B O ∢ = 90^{\circ}

, azaz:

A O

O_{1}

kör érintője az

A

pontban. Hasonlóan mutatható ki, hagy

A O ⊥ A O_{2}

vagyis

A O

O_{2}

kör érintője is az

A

pontban. Mivel így az

O_{1}

és

O_{2}

köröknek a közös

A

pontjukban közös érintőjük van, az

O_{1}

és

O_{2}

körök egymást érintik az

A

pontban.

2^{\circ}

O_{1} B O ▵ \sim B A C ▵

; ugyanis mind a kettő derékszögű és

O_{1} O B ∢ = A C B ∢

. Ebből folyik:

\begin{matrix} O_{1} B : B O = A B : A C, tehát O_{1} B = \frac{A B \cdot B O}{A C} = \frac{A B \cdot B C}{2 A C} . \\ Hasonlóan O_{2} C O ▵ \sim C A B ▵ és O_{2} C = \frac{A C \cdot B C}{2 A B} . \\ Ha már most A B = c, A C = b, B C = \sqrt[]{b^{2} + c^{2}}, tehát \\ O_{1} B = \frac{c \sqrt[]{b^{2} + c^{2}}}{2 b} és O_{2} C = \frac{b \sqrt[]{b^{2} + c^{2}}}{2 c} . \end{matrix}

Láng Géza (Ág. ev. Rudolf rg. V. o. Békéscsaba)