Feladat:	512. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Alpár L. ,  Balassa Gy. ,  Bársony S. ,  Blazsek I. ,  Budó Ágoston ,  Busztin A. ,  Böszörményi M. ,  Erdélyi Erzsi ,  Ernst F. ,  Faragó S. ,  Gajzágó E. ,  Gerber Edit ,  Gohn E. ,  Holczmann V. ,  Jancsek J. ,  Kemény I. ,  Kiss György ,  Klein Béla ,  Kövesdi D. ,  Lázár D. ,  Nay A. ,  Perlesz Gy. ,  Prém L. ,  Scheibner K. ,  Sebők Gy. ,  Semmelweiss O. ,  Singer Gy. ,  Szabó Piroska ,  Varga Á. ,  Vezér Gy.
Füzet:	1930/április, 240 - 241. oldal		PDF  |  MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Beírt kör, Beírt kör középpontja, Síkgeometriai számítások trigonometria nélkül háromszögekben, Szinusztétel alkalmazása, Koszinusztétel alkalmazása, Gyakorlat
Hivatkozás(ok):	Feladatok: 1930/február: 512. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.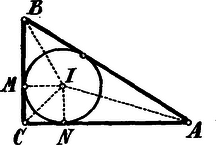   I. Megoldás. A derékszögű háromszögbe írt kör sugara $\begin{array}{c}{\displaystyle r=\frac{a+b-c}{2}\mathrm{,}}\end{array}$ ahol $a$ és $b$ a derékszögei háromszög befogói, $c$ pedig az átfogója. Legyen $M$ a kör érintési pontja a $BC=a$, $N$ az $AC=b$ oldalon. ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\overline{CI}}^2={\overline{CN}}^2+{\overline{IN}}^2=2r^2=2{\left(\frac{a+b-c}{2}\right)}^2=\frac{a^2+b^2+c^2+2ab-2\left(a+b\right)c}{2}=}\hfill \\ \hfill {\displaystyle =\frac{2c^2+2ab-2\left(a+b\right)c}{2}=c^2-\left(a+b\right)c+ab=\left(c-a\right)\left(c-b\right)\mathrm{.}}\hfill \\ \hfill {\displaystyle {\overline{BI}}^2={\overline{BM}}^2+{\overline{MI}}^2={\left(a-r\right)}^2+r^2=a^2-2ar+2r^2=}\hfill \\ \hfill {\displaystyle =a^2-\left(a+b-c\right)a+\left(c-a\right)\left(c-b\right)=\left(c-b\right)a+\left(c-a\right)\left(c-b\right)=\left(c-b\right)c\mathrm{.}}\hfill \end{array}}$ Hasonlóan ${\overline{AI}}^2=\left(c-a\right)c$. ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{1}{{\overline{AI}}^2}+\frac{1}{{\overline{BI}}^2}+\frac{\sqrt[]{2}}{AI\cdot BI}=\frac{1}{\left(c-a\right)c}+\frac{1}{\left(c-b\right)c}+\frac{\sqrt[]{2}}{c\sqrt[]{\left(c-a\right)\left(c-b\right)}}=}\hfill \\ \hfill {\displaystyle =\frac{c-b+c-a+\sqrt[]{2\left(c-a\right)\left(c-b\right)}}{c\left(c-a\right)\left(c-b\right)}=\frac{2c-a-b+\sqrt[]{2\cdot {\overline{CI}}^2}}{c\left(c-a\right)\left(c-b\right)}=}\hfill \\ \hfill {\displaystyle =\frac{2c-a-b+2r}{c\left(c-a\right)\left(c-b\right)}=\frac{2c-a-b+a+b-c}{c\left(c-a\right)\left(c-b\right)}=\frac{1}{\left(c-a\right)\left(c-b\right)}=\frac{1}{{\overline{CI}}^2}\mathrm{.}}\hfill \end{array}}$   Klein Béla (Kölcsey Ferenc rg. VII. o. Bp. VI.)   II. Megoldás. Az $ACI\sphericalangle ={45}^{\circ }$, az $AIB\sphericalangle ={180}^{\circ }-\left(\frac{\alpha }{2}+\frac{\beta }{2}\right)={180}^{\circ }-{45}^{\circ }={135}^{\circ }$. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle \text{<span style="font-weight: normal;font-style: normal;">Az</span>}ACI▵\text{<span style="font-weight: normal;font-style: normal;">-ből:</span>}AI:CI=\text{sin}{45}^{\circ }:\text{sin}\frac{\alpha }{2}\mathrm{.}}\hfill \\ \hfill {\displaystyle }& {\displaystyle \text{<span style="font-weight: normal;font-style: normal;">Az</span>}ABI▵\text{<span style="font-weight: normal;font-style: normal;">-ből:</span>}AB:BI=\text{sin}{135}^{\circ }:\text{sin}\frac{\alpha }{2}\mathrm{.}}\hfill \end{array}}$ Minthogy $\text{sin}{135}^{\circ }=\text{sin}{45}^{\circ }$, keletkezik: $\begin{array}{c}{\displaystyle AI:CI=AB:BI\text{<span style="font-weight: normal;font-style: normal;">és innen</span>}\frac{1}{{\overline{CI}}^2}=\frac{{\overline{AB}}^2}{\overline{A{I}^{2}B{I}^2}}\mathrm{.}}\end{array}$ (1) Alkalmazzuk az $ABI▵$ $AB$ oldalára a cosinus tételt: mivel $\text{cos}{135}^{\circ }=-\text{cos}{45}^{\circ }=-\frac{1}{2}\sqrt[]{2}$, lesz: $\begin{array}{c}{\displaystyle A{B}^2={\overline{AI}}^2+{\overline{BI}}^2+\overline{AI}\cdot \overline{BI}\cdot \sqrt[]{2}}\end{array}$ Helyettesítve ${\overline{AB}}^2$ ezen értékét (1)-be: $\begin{array}{c}{\displaystyle \frac{1}{{\overline{CI}}^2}=\frac{1}{{\overline{BI}}^2}+\frac{1}{{\overline{AI}}^2}+\frac{\sqrt[]{2}}{\overline{AI}\cdot \overline{BI}}\mathrm{.}}\end{array}$ Kiss György (Berzsenyi Dániel rg. VI. o. Bp.)