Kezdőlap


Feladat:	500. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Alpár L. , Bársony S. , Braun Ernő , Busztin A. , Deutsch E. , Deutsch I. , Dux K. , Ehrenfeld Gy. , Fleischmann S. , Friedländer T. , Fröhlich K. , Gajzágó E. , Gárdos Gy. , Gerber Zs. , Grega B. , Hirschl J. , Holczmann V. , Kemény I. , Papp Zs. , Prém L. , Róna I. , Sparber P. , Szabó F. , Székely I. , Varga Á. , Vezér Gy.
Füzet:	1930/március, 211. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Síkgeometriai számítások trigonometria nélkül körökben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1930/január: 500. matematika gyakorlat

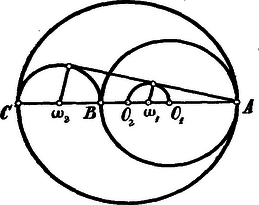
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az adott körök sugarai legyenek: $O_{1} A = r_{1}$ és $O_{2} A = r_{2}$ , tehát $O_{1} O_{2} = r_{2} - r_{1}$ és $B C = 2 (r_{2} - r_{1})$ . Az $O_{1} O_{2}$ mint átmérő fölött szerkesztett kör középpontja legyen $ω_{1}$ , sugara $\frac{O_{1} O_{2}}{2} = \frac{r_{2} - r_{1}}{2}$ és

\begin{matrix} ω_{1} A = \frac{r_{2} - r_{1}}{2} + r_{1} = \frac{r_{2} + r_{1}}{2} . \end{matrix}

B C

, mint átmérő fölött szerkesztett kör középpontja legyen

ω_{2}

, sugara:

\frac{B C}{2} = r_{2} - r_{1}

és

\begin{matrix} ω_{2} A = r_{2} - r_{1} + 2 r_{1} = r_{2} + r_{1} = 2 \bar{ω_{1} A} . \end{matrix}

Ha közös külső érintőjükre, mely az

O_{1} O_{2}

egyenest

A'

-ben metszi

ω_{1}

-ből és

ω_{2}

-ből merőlegeseket állítunk, akkor az így keletkező derékszögű háromszögek hasonlóságából folyik, hogy

\begin{matrix} \bar{ω_{1} A'} : \bar{ω_{2} A'} = \frac{O_{1} O_{2}}{2} : \frac{B C}{2} = 1 : 2. \end{matrix}

Mivel pedig

\bar{ω_{1} A'} : \bar{ω_{2} A'} = 1 : 2

, az

A'

pont az

A

ponttal összeesik.

Braun Ernő (Dobó István r. VI. o. Eger)