Feladat: 488. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Almási L. ,  Alpár L. ,  Antal Gy. ,  Atlasz Gy. ,  Braun E. ,  Braun Gy. ,  Busztin Anna ,  Deutsch E. ,  Deutsch I. ,  Dux Klára ,  Ehrenfeld Gy. ,  Emődy M. ,  Fejér B. ,  Fekete K. ,  Fleischmann S. ,  Fröhlich K. ,  Gajzágó E. ,  Gál I. ,  Gerber Zsuzsa ,  Gonosza I. ,  Haiman Gy. ,  Hartstein S. ,  Hirschl J. ,  Horváth L. ,  Kálnoky P. ,  Kazár Gy. ,  Kepes F. ,  Király Gy. ,  Kiss Gy. ,  Laufer M. ,  Magyar Margit ,  Máté P. ,  Meller P. ,  Papp Zs. ,  Parti I. ,  Polgár Gabriella ,  Prém L. ,  Radnai P. ,  Réfi B. ,  Reiner I. ,  Rózsa I. ,  Singer I. ,  Szabó Ferenc ,  Székely I. ,  Szőke J. ,  Vadász A. ,  Váradi L. ,  Varga Á. ,  Vas I. ,  Vezér E. ,  Vezér Gy. 
Füzet: 1930/február, 180. oldal  PDF  |  MathML 
Témakör(ök): Körülírt kör, Húrnégyszögek, Gyakorlat
Hivatkozás(ok):Feladatok: 1929/december: 488. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladatban foglalt utasítások szerint eljárva, DE az AC oldalt az F pontban AE a BC oldalt a H pontban metszi.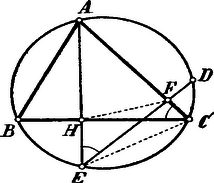

 
 

Az ACH és AEF háromszögeknek az A csúcsnál közös szögük van és mivel AD^=AB^, azért ACB∢ és AED∢ egyenlő kerületi szögek. Így tehát
AHC∢=AFE∢=90∘,azazAE⊥BC.

Szabó Ferenc (Kegyesrendi g. VI. o. Veszprém)
 

Jegyzet: A megoldások kizárólag azt az esetet tartották szem előtt, amidőn AB<AC, úgy hogy a D pont A és C közé esik. Megeshetik azonban, hogy AB>AC és a D pont úgy esik a B és C közé, hogy az E pont a D és F között van. Mindegyik esetben azonban CEHF négyszög húrnégyszög és ezért CHE∢=EFC∢=90∘.
Az 1. ábrában CEHF húrnégyszög, mert ACB∢=AED∢, azaz FH távolság C és E pontokból egyenlő szögek alatt látható.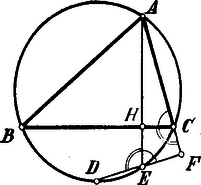
 
 

A 2. ábrában CHEF húrnégyszög, mert AED∢=180∘-ACB∢. Eszerint HEF∢=ACB∢ és HEF∢+HCF∢=180∘.